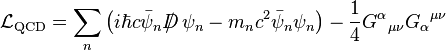Some details for Foundations of cosmology

Home

Contents

General relativity: field equations. 1

Quantum theory: some equations. 2

Schrödinger: 2

Klein-Gordon. 2

Dirac: Lorentz Invariant form.. 2

Pauli 3

Quantum electrodynamics. 3

Quantum chromodynamics. 3

Some details for roundations of cosmology

General relativity: field equations

With thanks to Wikipedia.

G_μνis symmetric:

where g_μν is the metric tensor.

The curvature scalar

$R=g^{\mu\nu}R_{\mu\nu}\,$

The Ricci tensor, R_μν is related to the more general Riemann curvature

$R_{\mu\nu}={R^\alpha}_{\mu\alpha\nu}.\,$

T_μν is the energy momentum tensor.

Quantum theory: some equations

With thanks to Wikipedia.

Schrödinger:

$i \hbar \frac{\partial}{\partial t}\Psi(\mathbf{r},t) = \hat H \Psi(\mathbf{r},t)$

Klein-Gordon

$\frac {1}{c^2} \frac{\partial^2}{\partial t^2} \psi - \nabla^2 \psi + \frac {m^2 c^2}{\hbar^2} \psi = 0.$

Dirac: Lorentz Invariant form

$i \hbar \gamma^\mu \partial_\mu \psi - m c \psi = 0$

Pauli

$\left[ \frac{1}{2m}(\boldsymbol{\sigma}\cdot(\mathbf{p} - q \mathbf{A}))^2 + q \phi \right] |\psi\rangle = i \hbar \frac{\partial}{\partial t} |\psi\rangle$

Quantum electrodynamics

The Lagrangian for a spin-1/2 field interacting with the electromagnetic field is given by the real part of

$\mathcal{L}=\bar\psi(i\gamma^\mu D_\mu-m)\psi -\frac{1}{4}F_{\mu\nu}F^{\mu\nu}$

where

$\gamma^\mu$ are Dirac matrices;

$\psi$ a bispinor field of spin-1/2 particles (e.g. electron–positron field);

$\bar\psi\equiv\psi^\dagger\gamma^0$ , called "psi-bar", is sometimes referred to as the Dirac adjoint;

$D_\mu \equiv \partial_\mu+ieA_\mu+ieB_\mu \,\!$ is the gauge covariant derivative;

e is the coupling constant, equal to the electric charge of the bispinor field;

m is the mass of the electron or positron;

$A_\mu$ is the covariant four-potential of the electromagnetic field generated by the electron itself;

$B_\mu$ is the external field imposed by external source;

$F_{\mu\nu} = \partial_\mu A_\nu - \partial_\nu A_\mu \,\!$ is the electromagnetic field tensor.

Quantum chromodynamics

The Lagrangian density is:

$\mathcal{L}_{\mathrm{QCD}} = \sum_n \left ( i\hbar c\bar\psi_n{D}\!\!\!\!/\ \psi_n - m_n c^2 \bar\psi_n \psi_n \right) - {1\over 4} G^\alpha {}_{\mu\nu} G_\alpha {}^{\mu\nu}$

D is the QCD gauge invariant derivative, n = 1 … 6, counts the quark types and Gαμν is the gluon field strength tensor.