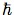(∂ψ/∂t) = Hψ
version history
|
Stanford Encyclopedia of PhilosophyA | B | C | D | E | F | G | H | I | J | K | L | M | N | O | P | Q | R | S | T | U | V | W | X | Y | Z
|
last substantive content
change
|
Bohmian mechanics inherits and makes explicit the nonlocality implicit in the notion, common to just about all formulations and interpretations of quantum theory, of a wave function on the configuration space of a many-particle system. It accounts for all of the phenomena governed by nonrelativistic quantum mechanics, from spectral lines and scattering theory to superconductivity, the quantum Hall effect and quantum computing. In particular, the usual measurement postulates of quantum theory, including collapse of the wave function and probabilities given by the absolute square of probability amplitudes, emerge from an analysis of the two equations of motion - Schrödinger's equation and the guiding equation - without the traditional invocation of a special, and somewhat obscure, status for observation.
It might seem, since it is widely agreed that any quantum mechanical system is completely described by its wave function, that quantum mechanics is fundamentally about the behavior of wave functions. Quite naturally, no physicist wanted this to be true more than did Erwin Schrödinger, the father of the wave function. Nonetheless, Schrödinger ultimately found this impossible to believe. His difficulty was not so much with the novelty of the wave function (Schrödinger 1935): "That it is an abstract, unintuitive mathematical construct is a scruple that almost always surfaces against new aids to thought and that carries no great message." Rather, it was that the "blurring" suggested by the spread out character of the wave function "affects macroscopically tangible and visible things, for which the term ‘blurring’ seems simply wrong."
For example, in the same paper Schrödinger noted that it may happen in radioactive decay that
the emerging particle is described ... as a spherical wave ... that impinges continuously on a surrounding luminescent screen over its full expanse. The screen however does not show a more or less constant uniform surface glow, but rather lights up at one instant at one spot ....And he observed that one can easily arrange, for example by including a cat in the system, "quite ridiculous cases" with
the ψ-function of the entire system having in it the living and the dead cat (pardon the expression) mixed or smeared out in equal parts.
It is thus because of the "measurement problem," of macroscopic superpositions, that Schrödinger found it difficult to regard the wave function as "representing reality." But then what does? With evident disapproval, Schrödinger describes how
the reigning doctrine rescues itself or us by having recourse to epistemology. We are told that no distinction is to be made between the state of a natural object and what I know about it, or perhaps better, what I can know about it if I go to some trouble. Actually -- so they say -- there is intrinsically only awareness, observation, measurement.
Many physicists pay lip service to the Copenhagen interpretation -- that quantum mechanics is fundamentally about observation or results of measurement. But it is becoming increasingly difficult to find any who, when pressed, will defend this interpretation. It seems clear that quantum mechanics is fundamentally about atoms and electrons, quarks and strings, not those particular macroscopic regularities associated with what we call measurements of the properties of these things. But if these entities are not to be somehow identified with the wave function itself -- and if talk of them is not merely shorthand for elaborate statements about measurements -- then where are they to be found in the quantum description?
There is, perhaps, a very simple reason why there has been so much difficulty discerning in the quantum description the objects we believe quantum mechanics should be describing. Perhaps the quantum mechanical description is not the whole story, a possibility most prominently associated with Albert Einstein.
In 1935 Einstein, Boris Podolsky and Nathan Rosen argued for this possibility in the famous EPR paper (Einstein et al. 1935), which they concluded with the following:
While we have thus shown that the wave function does not provide a complete description of the physical reality, we left open the question of whether or not such a description exists. We believe, however, that such a theory is possible.The argument given in the EPR paper for this conclusion invoked quantum correlations and an assumption of locality. (See the entry on quantum entanglement and information.)
Later, on the basis of more or less the same considerations as those of Schrödinger quoted above, Einstein again concluded that the wave function does not provide a complete description of individual systems, an idea he called "this most nearly obvious interpretation" (Einstein 1949, p. 672). In relation to a theory incorporating a more complete description, Einstein remarked that "the statistical quantum theory would ... take an approximately analogous position to the statistical mechanics within the framework of classical mechanics." It is perhaps worth noting here that Bohmian mechanics, as we shall see, exactly fits this description.
It is therefore not, as is often assumed, a question of a re-interpretation of quantum mechanics -- the present system of quantum mechanics would have to be objectively false, in order that another description of the elementary processes than the statistical one be possible.This claim of von Neumann was almost universally accepted among physicists and philosophers of science. For example, Max Born, who formulated the statistical interpretation of the wave function, assured us that (Born 1949, p. 109)
No concealed parameters can be introduced with the help of which the indeterministic description could be transformed into a deterministic one. Hence if a future theory should be deterministic, it cannot be a modification of the present one but must be essentially different.
Bohmian mechanics is, quite clearly, a counterexample to the claims of von Neumann, so something has to be wrong with von Neumann's argument. In fact, according to John Bell (Mermin 1993, p. 805), von Neumann's assumptions (about the relationships among the values of quantum observables that must be satisfied in a hidden-variables theory) are so unreasonable that the "the proof of von Neumann is not merely false but foolish!" Nonetheless, some physicists continue to rely on von Neumann's proof, although in recent years it is more common to find physicists citing the Kochen-Specker Theorem and, more frequently, Bell's inequality as the basis of this refutation. We still find, a quarter of a century after the rediscovery of Bohmian mechanics in 1952, statements such as these (Wigner 1976):
The proof he [von Neumann] published ..., though it was made much more convincing later on by Kochen and Specker, still uses assumptions which, in my opinion, can quite reasonably be questioned. ... In my opinion, the most convincing argument against the theory of hidden variables was presented by J. S. Bell (1964).
Now there are many more statements of a similar character that could have been cited. This quotation owes its significance to the fact that Wigner was not only one of the leading physicists of his generation, but, unlike most of his contemporaries, he was also profoundly concerned with the conceptual foundations of quantum mechanics and wrote on the subject with great clarity and insight.
There was, however, one physicist who wrote on this subject with even greater clarity and insight than Wigner himself, namely the very J. S. Bell whom Wigner praises for demonstrating the impossibility of a deterministic completion of quantum theory such as Bohmian mechanics. Here's how Bell himself reacted to Bohm's discovery (Bell 1987, p. 160):
But in 1952 I saw the impossible done. It was in papers by David Bohm. Bohm showed explicitly how parameters could indeed be introduced, into nonrelativistic wave mechanics, with the help of which the indeterministic description could be transformed into a deterministic one. More importantly, in my opinion, the subjectivity of the orthodox version, the necessary reference to the ‘observer,’ could be eliminated. ...But why then had Born not told me of this ‘pilot wave’? If only to point out what was wrong with it? Why did von Neumann not consider it? More extraordinarily, why did people go on producing ‘‘impossibility’’ proofs, after 1952, and as recently as 1978? ... Why is the pilot wave picture ignored in text books? Should it not be taught, not as the only way, but as an antidote to the prevailing complacency? To show us that vagueness, subjectivity, and indeterminism, are not forced on us by experimental facts, but by deliberate theoretical choice?
Wigner to the contrary notwithstanding, Bell did not establish the impossibility of a deterministic reformulation of quantum theory, nor did he ever claim to have done so. On the contrary, over the course of the past several decades, until his untimely death in 1990, Bell was the prime proponent, for a good part of this period almost the sole proponent, of the very theory, Bohmian mechanics, that he is supposed to have demolished.
Bohmian mechanics is of course as much a counterexample to the Kochen-Specker argument for the impossibility of hidden variables as it is to the one of von Neumann. It is obviously a counterexample to any such argument. However reasonable the assumptions of such an argument, some of them must fail for Bohmian mechanics.
Wigner was quite right to suggest that the assumptions of Kochen and Specker are more convincing than those of von Neumann. They appear, in fact, to be quite reasonable indeed . However, they are not. The impression that they are arises from a pervasive error, a naive realism about operators, that will be discussed below in the sections on quantum observables, on spin, and on contextuality.
One of the achievements of John Bell was to replace the "arbitrary axioms" (Bell 1987, page 11) of Kochen-Specker and others by an assumption of locality, of no action-at-a-distance. It would be hard to argue against the reasonableness of such an assumption, even if one were so bold as to doubt its inevitability. Bell showed that any hidden-variables formulation of quantum mechanics must be nonlocal, as, indeed, Bohmian mechanics is. But he showed much much more.
In a celebrated paper published in 1964, Bell showed that quantum theory itself is irreducibly nonlocal. This fact about quantum mechanics, based as it is on a short and mathematically simple analysis, could have been recognized soon after the discovery of quantum theory in the 1920's. That this did not happen is no doubt due in part to the obscurity of orthodox quantum theory and to the ambiguity of its commitments. It was, in fact, his examination of Bohmian mechanics that led Bell to his nonlocality analysis. In the course of his investigation of Bohmian mechanics he observed that (Bell 1987, p. 11):
in this theory an explicit causal mechanism exists whereby the disposition of one piece of apparatus affects the results obtained with a distant piece.In a footnote, Bell added that "Since the completion of this paper such a proof has been found." This proof was published in his 1964 paper, "On the Einstein-Podolsky-Rosen Paradox," in which he derives Bell's inequality, the basis of his conclusion of quantum nonlocality. (For a discussion of how nonlocality emerges in Bohmian mechanics, see Section 13.)Bohm of course was well aware of these features of his scheme, and has given them much attention. However, it must be stressed that, to the present writer's knowledge, there is no proof that any hidden variable account of quantum mechanics must have this extraordinary character. It would therefore be interesting, perhaps, to pursue some further "impossibility proofs," replacing the arbitrary axioms objected to above by some condition of locality, or of separability of distant systems.
It is worth stressing that Bell's analysis indeed shows that any account of quantum phenomena must be nonlocal, not just any hidden variables account. Bell showed that nonlocality is implied by the predictions of standard quantum theory itself. Thus if nature is governed by these predictions, then nature is nonlocal. [That nature is so governed, even in the crucial EPR-correlation experiments, has by now been established by a great many experiments, the most conclusive of which is perhaps that of Aspect (Aspect et al., 1982).]
Bell, too, stressed this point (by determinism Bell here means hidden variables):
It is important to note that to the limited degree to which determinism plays a role in the EPR argument, it is not assumed but inferred. What is held sacred is the principle of ‘local causality’ -- or ‘no action at a distance’...It is remarkably difficult to get this point across, that determinism is not a presupposition of the analysis. (Bell 1987, p. 143)
Despite my insistence that the determinism was inferred rather than assumed, you might still suspect somehow that it is a preoccupation with determinism that creates the problem. Note well then that the following argument makes no mention whatever of determinism. ... Finally you might suspect that the very notion of particle, and particle orbit ... has somehow led us astray. ... So the following argument will not mention particles, nor indeed fields, nor any other particular picture of what goes on at the microscopic level. Nor will it involve any use of the words ‘quantum mechanical system’, which can have an unfortunate effect on the discussion. The difficulty is not created by any such picture or any such terminology. It is created by the predictions about the correlations in the visible outputs of certain conceivable experimental set-ups. (Bell 1987, p. 150)
The "problem" and "difficulty" to which Bell refers above is the conflict between the predictions of quantum theory and what can be inferred, call it C, from an assumption of locality in Bohm's version of the EPR argument, a conflict established by Bell's inequality. C happens to concern the existence of a certain kind of hidden variables, what might be called local hidden variables, but this fact is of little substantive importance. What is important is not so much the identity of C as the fact that C is incompatible with the predictions of quantum theory. The identity of C is, however, of great historical significance: It is responsible for the misconception that Bell proved that hidden variables are impossible, a belief until recently almost universally shared by physicists, as well as for the view, even now almost universally held, that what Bell's result does is to rule out local hidden variables, a view that is misleading.
Here again is Bell, expressing the logic of his two-part demonstration of quantum nonlocality, the first part of which is Bohm's version of the EPR argument:
Let me summarize once again the logic that leads to the impasse. The EPRB correlations are such that the result of the experiment on one side immediately foretells that on the other, whenever the analyzers happen to be parallel. If we do not accept the intervention on one side as a causal influence on the other, we seem obliged to admit that the results on both sides are determined in advance anyway, independently of the intervention on the other side, by signals from the source and by the local magnet setting. But this has implications for non-parallel settings which conflict with those of quantum mechanics. So we cannot dismiss intervention on one side as a causal influence on the other. (Bell 1987, p. 149)
Not long after Schrödinger's discovery, in 1926, of wave mechanics, i.e., of Schrödinger's equation, Louis de Broglie in effect discovered Bohmian mechanics: In 1927, de Broglie found an equation of particle motion equivalent to the guiding equation for a scalar wave function (de Broglie 1928, p. 119), and he explained at the 1927 Solvay Congress how this motion could account for quantum interference phenomena. However, de Broglie responded poorly to an objection of Wolfgang Pauli (Pauli 1928) concerning inelastic scattering, no doubt making a rather bad impression on the illustrious audience gathered for the occasion.
Born and de Broglie very quickly abandoned the pilot-wave approach and became enthusiastic supporters of the rapidly developing consensus in favor of the Copenhagen interpretation. Bohmian mechanics was rediscovered in 1952 by David Bohm (Bohm 1952), the first person genuinely to understand its significance and implications. Its principal proponent during the sixties, seventies and eighties was John Bell.
Bohmian mechanics is the minimal completion of Schrödinger's equation, for a nonrelativistic system of particles, to a theory describing a genuine motion of particles. For Bohmian mechanics the state of a system of N particles is described by its wave function ψ = ψ(q1,...,qN) = ψ(q), a complex (or spinor) valued function on the space of possible configurations q of the system, together with its actual configuration Q defined by the actual positions Q1,...,QN of its particles. The theory is then defined by two evolution equations: Schrödinger's equation
ifor ψ(t), where H is the nonrelativistic (Schrödinger) Hamiltonian, containing the masses of the particles and a potential energy term, and a first-order evolution equation,
The Guiding Equation:for Q(t), the simplest first-order evolution equation for the positions of the particles that is compatible with the Galilean (and time-reversal) covariance of the Schrödinger evolution (Dürr et al. 1992, pp. 852-854). Here
dQk/dt = (
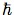is Planck's
constant divided by 2π, mk is the mass of the k-th
particle, and ∂k is the gradient with respect to the
coordinates of the k-th particle. If ψ is spinor-valued, the products
in numerator and denominator should be understood as scalar products. If
external magnetic fields are present, the gradient should be understood as the
covariant derivative, involving the vector potential. (Since the denominator on
the right hand side of the guiding equation vanishes at the nodes of ψ, global
existence and uniqueness for the Bohmian dynamics is a nontrivial matter. It is
proven in Berndl, Dürr, et al. 1995.)
For an N-particle system these two equations (together with the detailed specification of the Hamiltonian, including all interactions contributing to the potential energy) completely define the Bohmian mechanics. This deterministic theory of particles in motion accounts for all the phenomena of nonrelativistic quantum mechanics, from interference effects to spectral lines (Bohm 1952, pp. 175-178) to spin (Bell 1964, p. 10), and it does so in an entirely ordinary manner, as we shall explain in the following sections.
The form of the guiding equation given above is, for a scalar wave function, describing particles without spin, a little more complicated than necessary, since the complex conjugate of the wave function, appearing in the numerator and the denominator, cancels. If one looks for an evolution equation for the configuration compatible with the space-time symmetries of Schrödinger's equation, one almost immediately arrives at the guiding equation in this simpler form as the simplest possibility.
However, the form given above has two advantages: First, it makes sense for particles with spin -- and all the apparently paradoxical quantum phenomena associated with spin are, in fact, thereby accounted for by Bohmian mechanics without further ado. Secondly, and this is crucial to the fact that Bohmian mechanics is empirically equivalent to orthodox quantum theory, the right hand side of the guiding equation is J/ρ, the ratio of the quantum probability current to the quantum probability density. This shows first of all that it should require no imagination whatsoever to guess the guiding equation from Schrödinger's equation, provided one is looking for one, since the classical formula for current is density times velocity. Moreover, it follows from the quantum continuity equation ∂ρ/∂t + div J = 0, an immediate consequence of Schrödinger's equation, that if at some time (say the initial time) the configuration Q of our system is random, with distribution given by |ψ|2 = ψ*ψ, this will be true at all times (so long as the system does not interact with its environment).
This demonstrates that all claims to the effect that the predictions of quantum theory are incompatible with the existence of hidden variables, with an underlying deterministic model in which quantum randomness arises from averaging over ignorance, are wrong. For Bohmian mechanics provides us with just such a model: For any quantum experiment we merely take as the relevant Bohmian system the combined system that includes the system upon which the experiment is performed as well as all the measuring instruments and other devices used in performing the experiment (together with all other systems with which these have significant interaction over the course of the experiment). The "hidden variables" model is then obtained by regarding the initial configuration of this big system as random in the usual quantum mechanical way, with distribution given by |ψ|2. The initial configuration is then transformed, via the guiding equation for the big system, into the final configuration at the conclusion of the experiment. It then follows that this final configuration of the big system, including in particular the orientation of instrument pointers, will also be distributed in the quantum mechanical way, so that this deterministic Bohmian model yields the usual quantum predictions for the results of the experiment.
As the preceding paragraph suggests, and as we discuss in more detail in later sections, in Bohmian mechanics there is no need -- and, indeed, no room -- for any "measurement postulates" or axioms governing the behavior of other "observables": Any such axioms would be at best redundant, and would quite possibly be inconsistent.
Bohmian mechanics has been presented here as a first-order theory, in which it is the velocity, the rate of change of position, that is fundamental: it is this quantity, given by the guiding equation, that is specified by the theory, directly and simply, with the second-order (Newtonian) concepts of acceleration and force, work and energy playing no fundamental role. Bohm, however, did not regard his theory in this way. He regarded it, fundamentally, as a second-order theory, describing particles moving under the influence of forces, among which, however, one must include a force stemming from a "quantum potential."
In his 1952 hidden-variables paper (Bohm 1952), Bohm arrived at his theory by writing the wave function in the polar form ψ = Rexp(iS/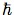), where S and R are
real, with R nonnegative, and rewriting Schrödinger's equation in terms
of these new variables to obtain a pair of coupled evolution equations: the
continuity equation for ρ = R2 and a modified
Hamilton-Jacobi equation for S, differing from the usual classical
Hamilton-Jacobi equation only by the appearance of an extra term, the
quantum potential
U = −∑k(alongside the classical potential energy term.
Bohm then used the modified Hamilton-Jacobi equation to define particle trajectories just as is done for the classical Hamilton-Jacobi equation, that is, by identifying ∂kS with mkvk, i.e., by setting
dQk/dt = ∂kS / mk,which is equivalent to the guiding equation for particles without spin. [Notice that in this form the guiding equation is already suggested by the (pre-Schrödinger equation) de Broglie relation p =
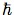k, as well as
by the eikonal equation of classical optics.] The resulting motion is precisely
what would be obtained classically if the particles were acted upon by, in
addition to the usual forces, the force generated by the quantum potential.
The quantum potential formulation of the de Broglie-Bohm theory is still fairly widely used. For example, the theory is presented in this way in the two existing monographs, by Bohm and Hiley and by Holland. And regardless of whether or not we regard the quantum potential as fundamental, it can in fact be quite useful. In order most simply to see that Newtonian mechanics should be expected to emerge from Bohmian mechanics in the classical limit, it is convenient to transform the theory into Bohm's Hamilton-Jacobi form. One then sees that the (size of the) quantum potential provides a measure of the deviation of Bohmian mechanics from its classical approximation. Moreover, the quantum potential can also be used to develop approximation schemes for solutions to Schrödinger's equation (Nerukh and Frederick 2000).
However, Bohm's rewriting of Schrödinger's equation in terms of variables that seem interpretable in classical terms does not come without a cost. The most obvious is increased complexity: Schrödinger's equation is rather simple, not to mention linear, whereas the modified Hamilton-Jacobi equation is somewhat complicated, and highly nonlinear -- and still requires the continuity equation for its closure. The quantum potential itself is neither simple nor natural. Even to Bohm it has seemed "rather strange and arbitrary" (Bohm 1980, p. 80). And it is not very satisfying to think of the quantum revolution as amounting to the insight that nature is classical after all, except that there is in nature what appears to be a rather ad hoc additional force term, the one arising from the quantum potential. The artificiality suggested by the quantum potential is the price one pays if one insists on casting a highly nonclassical theory into a classical mold.
Moreover, the connection between classical mechanics and Bohmian mechanics that is suggested by the quantum potential is rather misleading. Bohmian mechanics is not simply classical mechanics with an additional force term. In Bohmian mechanics the velocities are not independent of positions, as they are classically, but are constrained by the guiding equation. In classical Hamilton-Jacobi theory we also have this equation for the velocity, but there the Hamilton-Jacobi function S can be entirely eliminated and the description in terms of S simplified and reduced to a finite-dimensional description, with basic variables the positions and the (unconstrained) momenta of all the particles, given by Hamilton's or Newton's equations.
It can be argued that the most serious flaw in the quantum potential formulation of Bohmian mechanics is that it gives a completely false impression of the lengths to which we must go in order to convert orthodox quantum theory into something more rational. The quantum potential suggests, and indeed it has often been stated, that in order to transform Schrödinger's equation into a theory that can, in what are often called "realistic" terms, account for quantum phenomena, many of which are dramatically nonlocal, we must add to the theory a complicated quantum potential of a grossly nonlocal character. It should be clear that such sentiments are inappropriate, since the quantum potential need not be mentioned in the formulation of Bohmian mechanics and in any case is merely a reflection of the wave function, which Bohmian mechanics does not add to but shares with orthodox quantum theory.
But Bohmian mechanics is just such a deeper explanation. It resolves the dilemma of the appearance, in one and the same phenomenon, of both particle and wave properties in a rather straightforward manner: Bohmian mechanics is a theory of motion describing a particle (or particles) guided by a wave. Here we have a family of Bohmian trajectories for the two-slit experiment.
While each trajectory passes through but one of the slits, the wave passes through both; the interference profile that therefore develops in the wave generates a similar pattern in the trajectories guided by this wave.
Figure 1: An ensemble of trajectories for the two-slit experiment, uniform in the slits.
(Adapted by Gernot Bauer from Philippidis et al. 1979.)
Compare Feynman's presentation with Bell's (Bell 1987, p. 191):
Is it not clear from the smallness of the scintillation on the screen that we have to do with a particle? And is it not clear, from the diffraction and interference patterns, that the motion of the particle is directed by a wave? De Broglie showed in detail how the motion of a particle, passing through just one of two holes in screen, could be influenced by waves propagating through both holes. And so influenced that the particle does not go where the waves cancel out, but is attracted to where they cooperate. This idea seems to me so natural and simple, to resolve the wave-particle dilemma in such a clear and ordinary way, that it is a great mystery to me that it was so generally ignored.
The most puzzling aspect of the two-slit experiment is perhaps the following: If, by any means whatsoever, one is able to determine through which slit the particle passes, the interference pattern will be destroyed. This dramatic effect of observation is, in fact, a simple consequence of Bohmian mechanics. To see this one need only carefully consider what determining the slit through which the particle passes should mean. In particular, one must recognize that this must involve interaction with another system that must also be included in the Bohmian mechanical analysis. This destruction of interference is related, naturally enough, to the Bohmian mechanical analysis of quantum measurement (Bohm 1952), and it occurs via the mechanism that leads, in Bohmian mechanics, to the "collapse of the wave function."
The problem is as follows. Suppose that the wave function of any individual system provides a complete description of that system. When we analyze the process of measurement in quantum mechanical terms, we find that the after-measurement wave function for system and apparatus arising from Schrödinger's equation for the composite system typically involves a superposition over terms corresponding to what we would like to regard as the various possible results of the measurement -- e.g., different pointer orientations. It is difficult to discern in this description of the after-measurement situation the actual result of the measurement -- e.g., some specific pointer orientation. But the whole point of quantum theory, and the reason we are to believe in it, is that it is supposed to provide a compelling, or at least an efficient, account of our observations, that is, of outcomes of measurements. In short, the measurement problem is this: Quantum theory implies that measurements typically fail to have outcomes of the sort the theory was created to explain.
By contrast, if, like Einstein, we regard the description provided by the wave function as incomplete, the measurement problem vanishes: With a theory or interpretation like Bohmian mechanics, in which the description of the after-measurement situation includes, in addition to the wave function, at least the values of the variables that register the result, there is no measurement problem. In Bohmian mechanics pointers always point.
The measurement problem is often expressed a little differently. It is noted that textbook quantum theory provides two rules for the evolution of the wave function of a quantum system: A deterministic dynamics given by Schrödinger's equation for when the system is not being "measured" or observed, and a random collapse of the wave function to an eigenstate of the "measured observable" for when it is. However, the objection continues, textbook quantum theory does not provide a coherent account of how these two apparently incompatible rules can be reconciled.
That this formulation of the measurement problem is more or less equivalent to the previous one should be reasonably clear: If a wave function provides a complete description of the after-measurement situation, the outcome of the measurement must correspond to a wave function describing the actual result, that is, a "collapsed" wave function. Hence the collapse rule. But it is difficult to take seriously the idea that those interactions between system and apparatus that we happen to call measurements should be governed by laws different from those governing all other interactions. Hence the apparently incompatibility of the two rules.
The second formulation of the measurement problem, though basically equivalent to the first one, suggests an important question: Can Bohmian mechanics itself provide a coherent account of how the two dynamical rules might be reconciled? How does Bohmian mechanics justify the use of the "collapsed" wave function in place of the original one? This question was answered in Bohm's first papers on Bohmian mechanics (Bohm 1952, Part I, Section 7, and Part II, Section 2). What would nowadays be called effects of decoherence, produced by interaction with the environment (air molecules, cosmic rays, internal microscopic degrees of freedom, etc.), make it extremely difficult for the component of the after-measurement wave function corresponding to the actual result of the measurement to develop significant overlap -- in the configuration space of the very large system that includes all systems with which the original system and apparatus come into interaction -- with the other components of the after-measurement wave function. But without such overlap the future evolution of the configuration of the system and apparatus is generated, to a high degree of accuracy, by that component all by itself. The replacement is thus justified as a practical matter. (See also Dürr et al. 1992, Section 5.)
It is widely believed by proponents of orthodox quantum theory that the measurement problem itself is somehow resolved by decoherence. It is not easy to understand this belief. In the first formulation of the measurement problem, nothing prevents us from including in the apparatus all sources of decoherence. But then there is no longer any room for decoherence to be in any way relevant to that argument. Be that as it may, one of the best descriptions of the mechanisms of decoherence, though not the word itself, was given by Bohm (Bohm 1952), who recognized its importance several decades before it became fashionable. (See also the encyclopedia entry on The Role of Decoherence in Quantum Mechanics.)
For the evolution of the wave function, Bohmian mechanics is formulated in terms of Schrödinger's equation alone. Nonetheless the textbook collapse rule is a consequence of the Bohmian dynamics. To appreciate this one should first note that, since observation implies interaction, a system under observation cannot be a closed system but rather must be a subsystem of a larger system that is closed, which we may take to be the entire universe, or any smaller more or less closed system that contains the system to be observed, the subsystem. The configuration Q of this larger system naturally splits into X, the configuration of the subsystem, and Y, the configuration of the environment of the subsystem.
Suppose the larger system has wave function Ψ = Ψ(q) = Ψ(x, y). According to Bohmian mechanics, the larger system is then completely described by Ψ, evolving according to Schrödinger's equation, together with X and Y. The question then arises -- and it is a critical question -- as to what should be meant by the wave function of the subsystem.
There is a rather obvious answer for this, a natural function of x that suitably incorporates the objective structure at hand, namely the conditional wave function
ψ(x) = Ψ(x, Y)obtained by plugging the actual configuration of the environment into the wave function of the larger system. (This definition is appropriate only for scalar wave functions; for particles with spin the situation would be a little more complicated.) It then follows immediately that the configuration of the subsystem obeys the guiding equation with the conditional wave function on its right hand side.
Moreover, taking into account the way that the conditional wave function depends upon time t
ψt(x) = Ψt(x, Yt)via the time dependence of Y as well as that of Ψ, it is not difficult to see (Dürr et al. 1992) that the conditional wave function obeys Schrödinger's equation for the subsystem when that system is suitably decoupled from its environment -- this is meant to imply, in particular, that Ψ has a special form, what might be called an effective product form (similar to but more general than the superposition produced in an "ideal quantum measurement"), in which case the conditional wave function of the subsystem is also called its effective wave function -- and, using the quantum equilibrium hypothesis, that it randomly collapses according to the usual quantum mechanical rules under precisely those conditions on the interaction between the subsystem and its environment that define an ideal quantum measurement.
It is perhaps worth noting that orthodox quantum theory lacks the resources, namely, the actual configuration of the environment, that make possible the definition of the conditional wave function. Indeed, from an orthodox point of view what should be meant by the wave function of a subsystem is entirely obscure.
It is nowadays a rather familiar fact that dynamical systems quite generally give rise to behavior of a statistical character, with the statistics given by the (or a) stationary probability distribution for the dynamics. So it is with Bohmian mechanics, except that for the Bohmian system stationarity is not quite the right concept, and it is rather the notion of equivariance that is relevant. A probability distribution ρψ on configuration space, depending upon the wave function ψ, is equivariant if
(ρψ)t = ρψ twhere the dependence on t on the right arises from Schrödinger's equation and on the left from the evolution on probability distributions arising from the flow induced by the guiding equation. Thus equivariance expresses the mutual compatibility, relative to ρψ, of the Schrödinger evolution of the wave function and the Bohmian motion of the configuration. It is an immediate consequence of the guiding equation and the quantum continuity equation that ρψ = |ψ(q)|2 is equivariant. It is perhaps helpful, in trying to understand the status in Bohmian mechanics of the quantum equilibrium distribution, to think of
quantum equilibrium, ρ = |ψ|2as roughly analogous to (classical)
thermodynamic equilibrium, ρ = exp(-H/kT) /Z,the probability distribution of the phase-space point of a system in equilibrium at temperature T. (Z is a normalization constant called the partition function and k is Boltzmann's constant.) This analogy has several facets: In both cases the probability distributions are naturally associated with their respective dynamical systems. In particular, these distributions are stationary or, what amounts to the same thing within the framework of Bohmian mechanics, equivariant. In both cases it appears natural to try to justify these equilibrium distributions by means of mixing-type, convergence-to-equilibrium arguments (Bohm 1953, Valentini 2001). In both cases the ultimate justification for these probability distributions must, arguably, be in terms of statistical patterns exhibited by ensembles of actual subsystems within a typical individual universe (Bell 1987, page 129, Dürr et al. 1992). (And in both cases the status of, and justification for, equilibrium distributions is still controversial.) It can be shown (Dürr et al. 1992) that probabilities for positions given by the quantum equilibrium distribution emerge naturally from an analysis of "equilibrium" for the deterministic dynamical system defined by Bohmian mechanics, in much the same way that the Maxwellian velocity distribution emerges from an analysis of classical thermodynamic equilibrium. (For more on the thermodynamic side of the analogy see Goldstein 2001.) Thus with Bohmian mechanics the statistical description in quantum theory indeed takes, as Einstein anticipated, "an approximately analogous position to the statistical mechanics within the framework of classical mechanics."
[I]n physics the only observations we must consider are position observations, if only the positions of instrument pointers. It is a great merit of the de Broglie-Bohm picture to force us to consider this fact. If you make axioms, rather than definitions and theorems, about the "measurement" of anything else, then you commit redundancy and risk inconsistency.Consider first classical mechanics. The observables are functions on phase space, functions of the positions and momenta of the particles. The theory is defined by the axioms governing the behavior of the basic observables -- Newton's equations for the positions or Hamilton's for positions and momenta. What would be the point of making additional axioms, for other observables? After all, the behavior of any observable is entirely determined by the behavior of the basic observables. For example, for classical mechanics, the principle of the conservation of energy is a theorem, not an axiom.
The situation might seem to be different in quantum mechanics, since in quantum mechanics there are no basic observables having the property that all other observables are functions of these. This is connected with the fact that in quantum mechanics, with its positivistic orientation, no observables are taken seriously as describing objective properties, as actually having values regardless of whether they are or have been measured. Rather, all talk of observables in quantum mechanics is supposed to be understood as talk about the measurement of the observables.
But if this is so, the situation with regard to other observables in quantum mechanics is not really that different from in classical mechanics. Whatever is supposed to be meant in quantum mechanics by the measurement of (the values of) observables -- that, we are urged to believe, don't actually have values -- it must at least refer to some experiment involving interaction between the "measured" system and a "measuring" apparatus leading to a recognizable result, as given potentially by, say, a pointer orientation. But then if the axioms that we do have suffice for the behavior of pointer orientations (at least when they are observed), rules about the measurement of other observables must be theorems, following from those axioms, not additional axioms.
It should be clear from the discussion towards the end of Section 4 and at the beginning of Section 9 that, assuming the quantum equilibrium hypothesis, any analysis of the measurement of a quantum observable for orthodox quantum theory -- whatever that may be taken to mean and however the corresponding experiment may be performed -- provides ipso facto at least as adequate an account for Bohmian mechanics. The only part of orthodox quantum theory relevant to the analysis is the Schrödinger evolution, and this it shares with Bohmian mechanics. The main difference in the two accounts is that the orthodox one encounters the measurement problem before reaching a satisfactory conclusion while the Bohmian account does not. This difference stems of course from what Bohmian mechanics adds to orthodox quantum theory: actual configurations.
In the rest of this section, I wish to touch upon the significance of quantum observables for Bohmian mechanics: on how they naturally emerge and what talk of them means. (It follows from what has been said in the three preceding paragraphs that what we conclude here about quantum observables for Bohmian mechanics holds for orthodox quantum theory as well.)
It happens that Bohmian mechanics leads to a natural association between experiments and so-called generalized observables, given by positive-operator-valued measures (Davies 1976), or POVM's, O(dz), on the value spaces for the results of the experiments (Berndl, Daumer, et al. 1995). This association is such that the probability distribution of the result Z of an experiment, when performed upon a system with wave function ψ, is given by <ψ | O(dz)ψ> (where < | > is the usual inner product between quantum state vectors).
Moreover, this conclusion is basically an immediate consequence of the very meaning of an experiment from a Bohmian perspective: a coupling of system to apparatus leading to a result Z that is a function of the final configuration of the total system, e.g., the orientation of a pointer. Analyzed in Bohmian mechanical terms, the experiment defines a map from the initial wave function of the system to the distribution of the result. It follows directly from the structure of Bohmian mechanics, and from the fact that the quantum equilibrium distribution is quadratic in the wave function, that this map is bilinear (or, more precisely, sesquilinear). Such a map is equivalent to a POVM.
The simplest example of a POVM is a standard quantum observable, corresponding to a self-adjoint operator A on the Hilbert space of quantum states (i.e., wave functions). For Bohmian mechanics, more or less every "measurement-like" experiment is associated with this special kind of POVM, and the familiar quantum measurement axiom that the distribution of the result of the "measurement of the observable A" is given by the spectral measure for A relative to the wave function (in the very simplest cases just the absolute squares of the so-called probability amplitudes) is thus obtained.
For a variety of reasons, it quickly became almost universal, after quantum mechanics was discovered, to speak of an experiment associated with an operator A in the manner just sketched as a measurement of the observable A, as if the operator somehow corresponded to a property of the system that is in some sense measured by that experiment. There is no greater source of confusion about the meaning and implications of quantum theory than this naive realism about operators (Daumer et al., 1997).
Spin is the canonical quantum observable having no classical counterpart,
reputed to be impossible to grasp in a nonquantum way. The source of the
difficulty is not so much that spin is quantized in the sense that its allowable
values form a discrete set (for a spin-1/2 particle, ±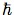/2) -- energy too may be quantized in
this sense -- nor even precisely that the components of spin in the different
directions fail to commute and so cannot be simultaneously discussed, measured,
imagined, or whatever it is that we are admonished not to do with noncommuting
observables. Rather the difficulty is that there is no ordinary (nonquantum)
quantity which, like the spin observable, is a 3-vector and which also is such
that its components in all possible directions belong to the same discrete set.
The problem, in other words, is that the usual vector relationships among the
various components of the spin vector are incompatible with the quantization
conditions on the values of these components.
For a particle of spin-1 the problem is even more severe. Since the components of spin in different directions aren't simultaneously measurable, the impossible vector relationships for the spin components of a quantum particle are not observable relationships. Simon Kochen and Ernst Specker (Kochen and Specker 1967) showed that for a spin-1 particle the squares of the spin components in the various directions satisfy, according to quantum theory, a collection of relationships, each individually observable, that taken together are impossible: the relationships are incompatible with the idea that measurements of these observables merely reveal their preexisting values rather than, as we are urged to believe in quantum theory, creating them. This Kochen-Specker Theorem continues to be regarded by many physicists and philosophers of physics as a definitive argument against the possibility of hidden variables.
We thus might naturally wonder how Bohmian mechanics manages to cope with spin. But this question has already been answered here. Bohmian mechanics makes sense for particles with spin, i.e., for particles whose wave functions are spinor-valued. When such particles are suitably directed toward Stern-Gerlach magnets, they emerge moving in more or less a discrete set of directions -- 2 possible directions for a spin-1/2 particle, having 2 spin components, 3 for spin-1 with 3 spin components, and so on. This occurs because the Stern-Gerlach magnets are so designed and so oriented that a wave packet (a localized wave function with reasonably well defined velocity) directed towards the magnet will, by virtue of the Schrödinger evolution, separate into distinct packets -- corresponding to the spin components of the wave function and moving in the discrete set of directions. The particle itself, depending upon its initial position, ends up in one of the packets moving in one of the directions.
The probability distribution for the result of such a Stern-Gerlach experiment is conveniently expressed in terms of the quantum mechanical spin operators -- for a spin-1/2 particle given by the Pauli spin matrices -- in the manner alluded to above. From a Bohmian perspective there is no hint of paradox in any of this unless we are seduced by naive realism about operators into insisting, despite its evident impossibility, that the spin operators correspond to genuine properties of the particles.
Even many Bohmians suggest that contextuality marks a significant departure from classical principles. For example, Bohm and Hiley (1993) write that "The context dependence of results of measurements is a further indication of how our interpretation does not imply a simple return to the basic principles of classical physics."
However, to understand contextuality from the perspective of Bohmian mechanics is to appreciate that almost nothing needs to be explained. Consider an operator A that commutes with operators B and C (which however don't commute with each other). What is often called the "result for A" in an experiment for "measuring A together with B" usually disagrees with the "result for A" in an experiment for "measuring A together with C" because, even if everything else is the same, these experiments are different and different experiments usually have different results. The misleading reference to measurement, with the associated naive realism about operators, makes contextuality seem more than it is.
If we avoid naive realism about operators, contextuality amounts to little more than the rather unremarkable observation that results of experiments should depend upon how they are performed, even when the experiments considered are associated with the same operator in the manner alluded to above. David Albert (Albert 1992, p. 153) has given a particularly simple and striking example of this dependence for Stern-Gerlach experiments "measuring" the z-component of spin. If one reverses the polarity in a magnet for "measuring" the z-component of spin, keeping the same geometry, one obtains another magnet for "measuring" the z-component of spin. The use of one or the other of these two magnets will often lead to opposite conclusions about the "value of the z-component of spin" prior to the "measurement" (for the same initial value of the position of the particle).
As Bell has insisted (Bell 1987, p. 166):
A final moral concerns terminology. Why did such serious people take so seriously axioms which now seem so arbitrary? I suspect that they were misled by the pernicious misuse of the word ‘measurement’ in contemporary theory. This word very strongly suggests the ascertaining of some preexisting property of some thing, any instrument involved playing a purely passive role. Quantum experiments are just not like that, as we learned especially from Bohr. The results have to be regarded as the joint product of ‘system’ and ‘apparatus,’ the complete experimental set-up. But the misuse of the word ‘measurement’ makes it easy to forget this and then to expect that the ‘results of measurements’ should obey some simple logic in which the apparatus is not mentioned. The resulting difficulties soon show that any such logic is not ordinary logic. It is my impression that the whole vast subject of ‘Quantum Logic’ has arisen in this way from the misuse of a word. I am convinced that the word ‘measurement’ has now been so abused that the field would be significantly advanced by banning its use altogether, in favour for example of the word ‘experiment.’
It should be emphasized that the nonlocality of Bohmian mechanics derives solely from the nonlocality built into the structure of standard quantum theory, as provided by a wave function on configuration space, an abstraction which, roughly speaking, combines -- or binds -- distant particles into a single irreducible reality. As Bell (Bell 1987, p. 115) has stressed,
That the guiding wave, in the general case, propagates not in ordinary three-space but in a multidimensional-configuration space is the origin of the notorious ‘nonlocality’ of quantum mechanics. It is a merit of the de Broglie-Bohm version to bring this out so explicitly that it cannot be ignored.
Thus the nonlocal velocity relation in the guiding equation is but one aspect of the nonlocality of Bohmian mechanics. There is also the nonlocality, or nonseparability, implicit in the wave function itself and in its propagation, a nonlocality that does not in fact assume the structure -- actual configurations -- that Bohmian mechanics adds to orthodox quantum theory. And as Bell has shown, using the connection between the wave function and the predictions of quantum theory concerning experimental results, this nonlocality cannot easily be argued away (see Section 2).
The nonlocality of Bohmian mechanics can be appreciated perhaps most efficiently, in all its aspects, by focusing on the conditional wave function. Suppose, for example, that in an EPR-Bohm experiment particle 1 passes through its Stern-Gerlach magnet before particle 2 arrives at its magnet. Then the orientation of the Stern-Gerlach magnet for particle 1 will have a significant effect upon the conditional wave function of particle 2: If the Stern-Gerlach magnet for particle 1 is so oriented as to "measure the z-component of spin," then after particle 1 has passed through its magnet the conditional wave function of particle 2 will be an eigenvector (or eigenstate) of the z-component of spin (in fact, belonging to the eigenvalue that is the negative of the one "measured" for particle 1), and the same thing is true for any other component of spin. You can dictate the kind of spin eigenstate produced for particle 2 by appropriately choosing the orientation of an arbitrarily distant magnet. As to the future behavior of particle 2, in particular how it is affected by its magnet, this of course depends very much on the character of its conditional wave function and hence is very strongly influenced by the choice of orientation of the distant magnet.
This nonlocal effect upon the conditional wave function of particle 2 follows from combining the standard analysis of the evolution of the wave function in the EPR-Bohm experiment with the definition of the conditional wave function. (For simplicity, we ignore permutation symmetry.) Before any magnets have been reached the EPR-Bohm wave function is a sum of two terms, corresponding to nonvanishing values for two of the four possible joint spin components for the two particles, each term a product of an eigenstate for a component of spin in a given direction for particle 1 with the opposite eigenstate (i.e., belonging to the eigenvalue that is the negative of the eigenvalue for particle 1) for the component of spin in the same direction for particle 2. Moreover, by virtue of its symmetry under rotations, it happens that the EPR-Bohm wave function has the property that any component of spin, i.e., any direction, can be used in this decomposition. (This property is very interesting.)
Decomposing the EPR-Bohm wave function using the component of spin in the direction associated with the magnet for particle 1, the evolution of the wave function as particle 1 passes its magnet is easy to grasp: The evolution of the sum is determined (using linearity) by that of its individual terms, and the evolution of each term by that of each of its factors. The evolution of the particle-1 factor leads to a displacement along the magnetic axis in the direction determined by the (sign of the) spin component (i.e., the eigenvalue), as described in the fourth paragraph of Section 11. Once this displacement has occurred (and is large enough) the conditional wave function for particle 2 will correspond to the term in the sum selected by the actual position of particle 1. In particular, it will be an eigenstate of the component of spin "measured by" the magnet for particle 1.
The nonlocality of Bohmian mechanics has a remarkable feature: it is screened by quantum equilibrium. It is a consequence of the quantum equilibrium hypothesis that the nonlocal effects in Bohmian mechanics don't yield observable consequences that are also controllable -- we can't use them to send instantaneous messages. This follows from the fact that, given the quantum equilibrium hypothesis, the observable consequences of Bohmian mechanics are the same as those of orthodox quantum theory, for which instantaneous communication based on quantum nonlocality is impossible (see Eberhard 1978). The importance of quantum equilibrium for obscuring the nonlocality of Bohmian mechanics has been stressed by Valentini (1991).
Like nonrelativistic quantum theory, of which it is a version, Bohmian mechanics is incompatible with special relativity, a central principle of physics: it is not Lorentz invariant. Nor can Bohmian mechanics easily be modified to become Lorentz invariant. Configurations, defined by the simultaneous positions of all particles, play too crucial a role in its formulation, the guiding equation defining an evolution on configuration space.
This difficulty with Lorentz invariance is intimately connected with the nonlocality in Bohmian mechanics. Since quantum theory itself, by virtue merely of the character of its predictions concerning EPR-Bohm correlations, is irreducibly nonlocal (see Section 2), one might expect considerable difficulty with the Lorentz invariance of orthodox quantum theory as well with Bohmian mechanics. For example, the collapse rule of textbook quantum theory blatantly violates Lorentz invariance. As a matter of fact, the intrinsic nonlocality of quantum theory presents formidable difficulties for the development of any (many-particle) Lorentz invariant formulation that avoids the vagueness of orthodox quantum theory (see Maudlin 1994).
A somewhat surprising, and I think correct, evaluation of the importance of the problem of Lorentz invariance was made by Bell in an interview with the philosopher Renée Weber, not long before he died. Referring to the paradoxes of quantum mechanics, Bell observed that "Those paradoxes are simply disposed of by the 1952 theory of Bohm, leaving as the question, the question of Lorentz invariance. So one of my missions in life is to get people to see that if they want to talk about the problems of quantum mechanics -- the real problems of quantum mechanics -- they must be talking about Lorentz invariance."
The most common view on the matter of Lorentz invariance and quantum nonlocality is that a detailed description of microscopic quantum processes, such as would be provided by an extension of Bohmian mechanics to the relativistic domain, must violate Lorentz invariance. In this view Lorentz invariance is an emergent symmetry obeyed by our observations -- a statistical consequence of quantum equilibrium that governs the results of quantum experiments. This is the opinion of Bohm and Hiley (1993), of Holland (1993), and of Valentini (2001).
However -- unlike nonlocality -- violation of Lorentz invariance is not inevitable. It should be possible, it seems, to construct a fully Lorentz invariant theory providing a detailed description of microscopic quantum processes. One way to do this is by means of additional Lorentz invariant dynamical structure, for example a suitable time-like 4-vector field, that permits the definition of a foliation of space-time into space-like hypersurfaces providing a Lorentz invariant notion of "evolving configuration" and along which nonlocal effects are transmitted. See Dürr et al. 1999 for a toy model. Another possibility that should not be dismissed is that a fully Lorentz invariant account of quantum nonlocality can be achieved without the invocation of additional structure, exploiting only what is already at hand, for example, light-cone structure.
Be that as it may, Lorentz invariant nonlocality would remain somewhat enigmatic. The issues are extremely subtle. For example, Bell (1987, page 155) rightly would find "disturbing ... the impossibility of ‘messages’ faster than light, which follows from ordinary relativistic quantum mechanics in so far as it is unambiguous and adequate for procedures we [emphasis added] can actually perform. The exact elucidation of concepts like ‘message’ and ‘we’, would be a formidable challenge." While quantum equilibrium and the absolute uncertainty that it entails (Dürr et al. 1992) may be of some help here, the situation remains puzzling.
I know that most men, including those at ease with problems of the highest complexity, can seldom accept even the simplest and most obvious truth if it be such as would oblige them to admit the falsity of conclusions which they have delighted in explaining to colleagues, which they have proudly taught to others, and which they have woven, thread by thread, into the fabric of their lives.
A great many objections have been and continue to be raised against Bohmian mechanics. Here are some of them: Bohmian mechanics makes predictions about results of experiments different from those of orthodox quantum theory so it is wrong. Bohmian mechanics makes the same predictions about results of experiments as orthodox quantum theory so it is untestable and therefore meaningless. Bohmian mechanics is mathematically equivalent to orthodox quantum theory so it is not really an alternative at all. Bohmian mechanics is more complicated than orthodox quantum theory, since it involves an extra equation. (This objection is based on the surprisingly common misconception that orthodox quantum theory is defined solely by Schrödinger's equation, and does not actually need as part of its formulation any of the measurement postulates found in textbook quantum theory. It is only within a many-worlds framework that this view could begin to make sense, but I strongly doubt that it makes sense even there.) Bohmian mechanics requires the postulation of a mysterious and undetectable quantum potential. Bohmian mechanics requires the addition to quantum theory of a mysterious pilot wave. Bohmian mechanics, as von Neumann has shown, can't possibly work. Bohmian mechanics, as Kochen and Specker have shown, can't possibly work. Bohmian mechanics, as Bell has shown, can't possibly work. Bohmian mechanics is a childish regression to discredited classical modes of thought. Bohmian trajectories are crazy, since they may be curved even when no classical forces are present. Bohmian trajectories are crazy, since a Bohmian particle may be at rest in stationary quantum states. Bohmian trajectories are crazy, since a Bohmian particle may be at rest in stationary quantum states, even when these are large-energy eigenstates. Bohmian trajectories are surrealistic. Bohmian mechanics, since it is deterministic, is incompatible with quantum randomness. Bohmian mechanics is nonlocal. Bohmian mechanics is unintuitive. Bohmian mechanics is the many-worlds interpretation in disguise. (For a bit of discussion of some of these objections, see the exchange of letters on Quantum Theory Without Observers, in the February 1999 issue of Physics Today, particularly the last four of the eight letters. A link is provided in the Other Internet Resources section below.)
Most of these objections have little or no merit. Some arise from naive realism about operators, some from the idea that, to the extent that the concepts of classical physics apply at all, the laws of classical physics are more or less a priori, some from an inability to grasp the point of Bohmian mechanics, and some from sheer ignorance.
It is perhaps worth mentioning that despite the empirical equivalence between Bohmian mechanics and orthodox quantum theory, there are a variety of experiments and experimental issues that don't fit comfortably within the standard quantum formalism but are easily handled by Bohmian mechanics. Among these are dwell and tunneling times (Leavens 1996), escape times and escape positions (Daumer et al. 1997a), scattering theory (Dürr et al., 2000), and quantum chaos (Cushing 1994, Dürr et al., 1992a).
There is one striking feature of Bohmian mechanics that is often presented as an objection but is better regarded as an important clue about the meaning of quantum mechanics: in Bohmian mechanics the wave function acts upon the positions of the particles but, evolving as it does autonomously via Schrödinger's equation, it is not acted upon by the particles. This point is discussed in D? al. 1997 and in Goldstein and Teufel 2001, where it is suggested that, from a deeper perspective than afforded by standard Bohmian mechanics or quantum theory, the wave function should be regarded as nomological, as an object for conveniently expressing the law of motion somewhat analogous to the Hamiltonian in classical mechanics, and that a time-dependent Schrödinger-type equation, from this deeper (cosmological) perspective, is merely phenomenological.
Bohmian mechanics does not account for phenomena such as pair creation and annihilation characteristic of quantum field theory. This is not an objection to Bohmian mechanics but merely a recognition that quantum field theory explains a great deal more than does nonrelativistic quantum mechanics, whether in orthodox or Bohmian form. It does, however, underline the need to find an adequate, if not compelling, Bohmian version of quantum field theory, and of gauge theories in particular, a problem that is pretty much wide open. Some rather tentative steps in this direction can be found in Bohm and Hiley 1993, Holland 1993, Bell 1987 (p. 173), and in some of the articles in Cushing et al. 1996. (For a general discussion of this issue and of the point and value of Bohmian mechanics, see the exchange of letters between Goldstein and Weinberg by following the link provided in the Other Internet Resources section below.)
| Sheldon
Goldstein oldstein@math.rutgers.edu |
A | B | C | D | E | F | G | H | I | J | K | L | M | N | O | P | Q | R | S | T | U | V | W | X | Y | Z
