version history
|
A | B | C | D | E | F | G | H | I | J | K | L | M | N | O | P | Q | R | S | T | U | V | W | X | Y | Z
| This document uses XHTML/Unicode to
format the display. If you think special symbols are not displaying
correctly, see our guide Displaying
Special Characters. | |
last substantive content
change
|
Epistemic Logic
Epistemic logic is the logic of knowledge and belief. It
provides insight into the properties of individual knowers, has provided a means
to model complicated scenarios involving groups of knowers and has improved our
understanding of the dynamics of inquiry.
Epistemic logic gets its start with the recognition that expressions like
‘knows that’ or ‘believes that’ have systematic properties that are amenable to
formal study. In addition to its relevance for traditional philosophical
problems, epistemic logic has many applications in computer science and
economics. Examples range from robotics, network security and cryptography
applications to the study of social and coalitional interactions of various
kinds.
Modern treatments of the logic of knowledge and belief grow out of the work
of a number of philosophers and logicians writing from 1948 through the 1950s.
Rudolf Carnap, Jerzy Los, Arthur Prior, Nicholas Rescher, G.H. von Wright and
others recognized that our discourse concerning knowledge and belief exhibits
systematic features that admit of an axiomatic-deductive treatment. Among the
many important papers that appeared in the 1950s, von Wright's seminal work
(1951) is widely recognized as having initiated the formal study of epistemic
logic as we know it today. Von Wright's insights were extended by Jaakko
Hintikka in his book Knowledge and Belief: An Introduction to the Logic of
the Two Notions (1962). In the 1980s and 1990s, epistemic logicians focused
on the logical properties of systems containing groups of knowers and later
still on the epistemic features of so-called "multi-modal" contexts.
While this article deals with modern developments, epistemic logic has a
venerable history. In De Sophisiticis Elenchis as well as in the
Prior and Posterior Analytics Aristotle mentions some aspects
of the logic of knowledge and belief. In the medieval period, Buridan, Duns
Scotus and Ockham extended Aristotle's insights in a series of detailed
reflections whose themes and problems would be familiar to contemporary
epistemic logicians (Boh 1993, Knuutila 1993).
Contemporary epistemic logic may appear quite technical and removed from
traditional epistemological reflections. However, it assumes as its starting
point some features of the logical behavior of epistemic concepts that are
completely obvious. For instance, claiming to know p and q
implies that you know q. Furthermore, most systems of epistemic logic
begin with an assumption similar to G.E. Moore's intuitively obvious observation
that one cannot coherently assert "p but I do not believe (know)
p". Additional assumptions that serve as the basis for most epistemic
logics include the recognition that knowledge implies veracity. If I know
p then p must be the case. Thus, commonsense observations
concerning the behavior of the term "knows that", have served as the starting
point for later technical developments.
For the most part, epistemic logic focuses on propositional knowledge. Here,
an agent or a group of agents bears the propositional attitude knowing
towards some proposition. So, when one says: "Zoë knows that there is a chicken
in the yard", one asserts that Zoë is the agent who bears the propositional
attitude knowing towards the proposition expressed by "there is a
chicken in the yard". Beyond straightforward propositional knowledge of this
kind, epistemic logic also suggests ways to systematize the logic of questions
and answers (Zoë knows why Murphy barked) and provides insight into the
relationships between multiple modes of identification (Zoë knows that this man
is the chief) and also perhaps even into questions of procedural "know-how".
Epistemic logicians have found ways to formally treat a wide variety of
knowledge claims in propositional terms.
Syntactically, the language of propositional epistemic logic is simply a
matter of augmenting the language of propositional logic with a unary epistemic
operator Kc such that
| KcA |
|
reads |
|
"Agent c knows A |
and similarly for belief
| BcA |
|
reads |
|
"Agent c believes A |
for some arbitrary proposition A.
Hintikka provided a semantic interpretation of epistemic and doxastic
operators which we can present in terms of standard possible world semantics
along the following lines (Hintikka 1962):
| KcA: |
in all possible worlds compatible with what c knows, it
is the case that A |
| BcA: |
in all possible worlds compatible with what c believes,
it is the case that A |
The basic assumption is that any ascription of propositional attitudes like
knowledge and belief, involves dividing the set of possible worlds in two: Those
worlds compatible with the attitude in question and those that are incompatible
with it.
The set of worlds accessible to an agent depends on his or her informational
resources at that instant. It is possible to capture this dependency by
introducing a relation of accessibility, R, on the set of possible
worlds. To express the idea that for agent c, the world w′ is
compatible with his information state, or accessible from the possible world
w which c is currently in, it is required that R
holds between w and w′. This relation is written Rww′
and reads “world w′ is accessible from w”. The world
w′ is said to be an epistemic or doxastic alternative
to world w for agent c, depending on whether knowledge or
belief is the considered attitude. Given the above semantical interpretation, if
a proposition A is true in all worlds which agent c considers
possible then c knows A.
A possible world semantics for a propositional epistemic logic with a single
agent c then consists of a frame 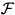 which in turn is a pair
<W,Rc> such that W is a
non-empty set of possible worlds and Rc is a binary
accessibility relation (relative to agent c) over W. A
model
which in turn is a pair
<W,Rc> such that W is a
non-empty set of possible worlds and Rc is a binary
accessibility relation (relative to agent c) over W. A
model 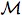 for an
epistemic system consists of a frame and a denotation function φ assigning sets
of worlds to atomic propositional formulas. Propositions are taken to be sets of
possible worlds; namely the set of possible worlds in which they are true. Let
atom be the set of atomic propositional formulae, then
φ : atom
for an
epistemic system consists of a frame and a denotation function φ assigning sets
of worlds to atomic propositional formulas. Propositions are taken to be sets of
possible worlds; namely the set of possible worlds in which they are true. Let
atom be the set of atomic propositional formulae, then
φ : atom 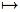 P(W), where P denotes the powerset operation. The
model
P(W), where P denotes the powerset operation. The
model 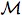 =
<W,Rc,φ> is called a Kripke-model
and the resulting semantics Kripke-semantics (Kripke 1963): An atomic
propositional formula, a, is said to be true in a world
w in
=
<W,Rc,φ> is called a Kripke-model
and the resulting semantics Kripke-semantics (Kripke 1963): An atomic
propositional formula, a, is said to be true in a world
w in 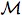 (written
(written 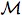 ,w
,w 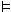 a) iff w is in
the set of possible worlds assigned to a, i.e.,
a) iff w is in
the set of possible worlds assigned to a, i.e., 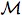 ,w
,w 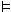 a iff w ∈
φ(a) for all a ∈ atom . The formula
KcA is true in an world w (i.e.,
a iff w ∈
φ(a) for all a ∈ atom . The formula
KcA is true in an world w (i.e.,
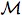 ,w
,w 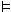 KcA) iff ∀w′∈W, if
Rcww′, then
KcA) iff ∀w′∈W, if
Rcww′, then 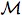 ,w′
,w′ 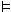 A. The semantics for the
Boolean connectives follow the usual recursive recipe. A modal formula is said
to be valid in a frame iff the formula is true for all possible
assignments in all worlds in the frame.
A. The semantics for the
Boolean connectives follow the usual recursive recipe. A modal formula is said
to be valid in a frame iff the formula is true for all possible
assignments in all worlds in the frame.
Similar semantics may be formulated for the belief operator. Since a belief
is not necessarily true but rather probably true, possibly true, or likely to be
true, we must modify our approach to the semantics of belief appropriately. For
instance, belief may be modeled by assigning a sufficiently high degree of
probability to the proposition in question and determining the doxastic
alternatives accordingly. The truth-conditions for the doxastic operator are
defined in a way similar to that of the knowledge operator and the model may
also be expanded to accommodate the two operators simultaneously.
An important feature of possible world semantics is that many common
epistemic axioms correspond to algebraic properties of the frame in the
following sense: A modal axiom is valid in a frame if and only if the
accessibility relation satisfies some algebraic condition. For example, the
axiom expressing the veridicality property that if a proposition is known by
c, then A is true,
(1) KcA → A,
is valid in all frames in which the accessibility relation is
reflexive in the sense that ∀w∈W : Rww.
Every possible world is accessible from itself. Similarly if the accessibility
relation satisfies the condition that ∀ w, w′, w″ ∈
W : Rww′ 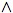 Rw′w″ → Rww″ then the axiom reflecting the idea that
the agent knows that he knows A if he does,
Rw′w″ → Rww″ then the axiom reflecting the idea that
the agent knows that he knows A if he does,
(2) KcA →
KcKcA,
is valid in all transitive frames. Other axioms of epistemic import
require yet other relational properties to be met in order to be valid in all
frames.
A nomenclature due to Lemmon (1977) and later refined by Bull and
Segerberg (1984) is helpful while cataloguing the axioms typically considered
interesting for epistemic logic (Table 1):
| K |
Kc(A→A′) →
(KcA →
KcA′) |
| D |
KcA →
¬Kc¬A |
| T |
KcA → A |
| 4 |
KcA →
KcKcA |
| 5 |
¬KcA →
Kc¬KcA |
| .2 |
¬Kc¬KcA
→
Kc¬Kc¬A |
| .3 |
Kc(KcA
→ KcA′) 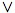 Kc(KcA′
→ KcA)
Kc(KcA′
→ KcA) |
| .4 |
A →
(¬Kc¬KcA
→ KcA) |
Table 1: Common Epistemic Axioms
These axioms in proper combinations make up epistemic modal systems of
varying strength depending on the modal formulas valid in the respective systems
given the algebraic properties assumed for the accessibility relation.
Although the axiom K by
itself constitutes the system K, the weakest system of
epistemic interest is usually considered to be system T. [Note:
The reader should take care to distinguish the epistemic operator K,
the modal axiom K and the
system of axioms K in what follows. Similarly, we distinguish
the axiom T from the system
T.] The system T includes the axioms T and K as valid axioms. Additional modal
strength may be obtained by extending T with other axioms drawn
from the above pool altering the frame semantics to validate the additional
axioms. By way of example, while KcA →
A is valid in system T,
KcA → A,
KcA →
KcKcA and
¬KcA →
Kc¬KcA are
all valid in S5 but not in T. System
T has a reflexive accessibility relation, S5
has an equivalence relation of accessibility. The arrows in Table 2 symbolize
that the system to which the arrow is pointing is included in the system from
which the arrow originates and hence reflect relative strength. Then
S5 is the strongest and S4 the weakest of the
ones listed.
Epistemic Systems
|
| KT4 |
= |
S4 |
|
| KT4 + .2 |
= |
S4.2 |
↑ |
| KT4 + .3 |
= |
S4.3 |
↑ |
| KT4 + .4 |
= |
S4.4 |
↑ |
| KT5 |
= |
S5 |
↑ |
Table 2: Relative Strength of Epistemic Systems Between S4 and
S5
One of the important tasks of epistemic logic is to catalogue all sound and
complete systems of such logics in order to allow us to pick the most
‘appropriate’ ones. The logics range from S4 over the
intermediate systems S4.2–S4.4 to
S5. By way of example, Hintikka settled for S4
(1962), Kutschera argued for S4.4 (1976), Lenzen suggested
S4.2 (1978), van der Hoek has proposed to strengthen knowledge
according to system S4.3 (1996). van Ditmarsch, van der Hoek
and Kooi together with Fagin, Halpern, Moses and Vardi (Fagin et al.
1995) and others assume knowledge to be S5 valid. Similar
completeness cataloguing is available for belief where axiom T is dropped and usually replaced by
D (to avoid the condition of
truth for belief but retain consistency among beliefs) yieding systems like
KD4–KD45 for belief. This also paves the way
for combining epistemic and doxastic systems and for studying the interplay
between knowledge and belief (see Voorbraak 1993). Care should be taken however
not to collapse knowledge and belief in the combined systems as have been noted
by Lenzen (1978) and Stalnaker (1996), among others.
A particularly malignant philosophical problem for epistemic logic is related
to closure properties. Axiom K,
can under certain circumstances be generalized to a closure property for an
agent's knowledge which is implausibly strong — logical
omniscience:
Whenever an agent c knows all of the
formulas in a set Γ and A follows logically from Γ,
then c also knows A.
In particular, c knows all theorems (letting Γ = ø), and he knows
all logical consequences of any formula which he knows (letting Γ consist of a
single formula). There are various ways of dealing with logical omniscience.
Some of the first proposals for solving the problem of logical omniscience
introduce semantical entities which explain why the agent appears to be, but in
fact is not really guilty of logical omniscience. These entities were called
‘impossible possible worlds’ by Hintikka (1975). The basic idea is that an agent
may mistakenly count among the worlds consistent with his or her knowledge, some
worlds containing logical contradictions. The mistake is simply a product of
limited resources; the agent may not be in a position to detect the
contradiction and may erroneously count them as genuine possibilities. Similar
entities called ‘seemingly possible’ worlds are introduced by Rantala (1975) in
his urn-model analysis of logical omniscience. Allowing impossible possible
worlds or seemingly possible worlds in which the semantic valuation of the
formulas is arbitrary to a certain extent provides a way of making the
appearance of logical omniscience less threatening. After all, on any realistic
account of epistemic agency, the agent is likely to consider (albeit
inadvertantly) worlds in which the laws of logic do not hold. Since no real
epistemic principles hold broadly enough to encompass impossible and seemingly
possible worlds, some conditions must be applied to epistemic models such that
they cohere with epistemic principles.
Computer scientists have proposed that what is being modelled in epistemic
logic is not knowledge simpliciter but a related concept which is
immune to logical omniscience. The epistemic operator
KcA should be read as ‘agent c
knows implicitly A’, ‘A follows from c's knowledge’,
‘A is agent c's possible knowledge’, etc. Propositional
attitudes like these should replace the usual ‘agent c knows
A’. While there exists some variation, the locutions all suggest
modeling implicit knowledge or what is implicitly represented in an
agent's information state rather than explicit knowledge (Fagin et
al. 1995, and others). The agents neither have to compute knowledge nor can
they be held responsible for answering queries based on their knowledge under
the implicit understanding of knowledge. Logical omniscience is an
epistemological condition for implicit knowledge, but the agent may actually
fail to realize this condition.
Single-agent systems may be extended to groups or multi-agent systems.
Following the standard treatment provided by Fagin, Halpern, Moses and Vardi
(Fagin et al. 1995) we can syntactically augment the language of
propositional logic with n knowledge operators, one for each agent
involved in the group of agents under consideration. The primary difference
between the semantics given for a mono-agent and a multi-agent semantics is
roughly that n accessibility relations are introduced. A modal system
for n agents is obtained by joining together n modal logics
where for simplicity it may be assumed that the agents are homogenous in the
sense that they may all be described by the same logical system. An epistemic
logic for n agents consists of n copies of a certain modal
logic. In such an extended epistemic logic it is possible to express that some
agent in the group knows a certain fact, that an agent knows that another agent
knows a fact etc. It is possible to develop the logic even further: Not only may
an agent know that another agent knows a fact, but they may all know this fact
simultaneously. From here it is possible to express that everyone knows that
everyone knows that everyone knows, that…. That it is common
knowledge.
As Lewis noted in his book Convention (1969) a convention requires
common knowledge among the agents that observe it. A variety of norms, social
and linguistic practices, agent interactions and games presuppose common
knowledge (Aumann 1994). A relatively simple way of defining common knowledge is
not to partition the group of agents into subsets with different common
‘knowledges’ but only to define common knowledge for the entire group of agents.
Once multiple agents have been added to the syntax, the language is augmented
with an additional operator c. CA is then interpreted as ‘It
is common knowledge among the agents that A’. Well-formed formulas
follow the standard recursive recipe with a few, but obvious, modifications
taking into account the multiple agents. An auxiliary operator E is
also introduced such that EA means ‘Everyone knows that A’.
EA is defined as the conjunction K1A 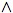 K2A
K2A 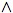 …
… 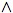 KnA.
KnA.
To semantically interpret n knowledge operators, binary
accessibility relations Rn are defined over the set
of possible worlds W. A special accessibility relation, R°, is
introduced to interpret the operator of common knowledge. The relation must be
flexible enough to express the relationship between individual and common
knowledge. The idea is to let the accessibility relation for c be the
transitive closure of the union of the accessibility relations corresponding to
the singular knowledge operators. The model 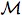 for an epistemic system with n
agents and common knowledge is accordingly a structure
for an epistemic system with n
agents and common knowledge is accordingly a structure 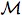 =
<W,R1,R2,…,Rn,R°,φ>,
where W is a non-empty space of possible worlds,
R1,R2,…,Rn,R°
are accessibility relations over W for which R° =
(R1 ∪ R2 ∪ … ∪
Rn) and φ again is the denotation function
assigning worlds to atomic propositional formula φ : atom
=
<W,R1,R2,…,Rn,R°,φ>,
where W is a non-empty space of possible worlds,
R1,R2,…,Rn,R°
are accessibility relations over W for which R° =
(R1 ∪ R2 ∪ … ∪
Rn) and φ again is the denotation function
assigning worlds to atomic propositional formula φ : atom 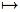 P(W). The
semantics for the Boolean connectives remain intact. The formula
KiA is true in a world w, i.e.,
P(W). The
semantics for the Boolean connectives remain intact. The formula
KiA is true in a world w, i.e.,
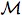 ,w
,w 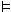 KiA iff ∀w′∈W : if
Riww′, then
KiA iff ∀w′∈W : if
Riww′, then 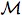 ,w′
,w′ 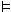 A. The formula CA is
true in a world w, i.e.,
A. The formula CA is
true in a world w, i.e., 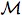 ,w
,w 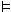 CA iff R°ww′
implies
CA iff R°ww′
implies 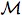 ,w′
,w′ 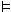 A. Varying the
properties of the accessibility relations
R1,R2,…,Rn,
as described above results in different epistemic logics. For instance system
K with common knowledge is determined by all frames, while
system S4 with common knowledge is determined by all reflexive
and transitive frames. Similar results can be obtained for the remaining
epistemic logics (Fagin et al. 1995).
A. Varying the
properties of the accessibility relations
R1,R2,…,Rn,
as described above results in different epistemic logics. For instance system
K with common knowledge is determined by all frames, while
system S4 with common knowledge is determined by all reflexive
and transitive frames. Similar results can be obtained for the remaining
epistemic logics (Fagin et al. 1995).
A significant difference between
alethic and epistemic logic is the introduction of the agent c to the
syntax. But what role does the agent play in epistemic logic? At the early
stages in the development of the logic they primarily served as indices on the
accessibility relation between possible worlds. However, there is nothing
particularly epistemic about being an index, and epistemic logicians soon began
recognizing the central role of the agent much more explicitly. An agent may
have knowledge which is S4.3 valid thereby obtaining a certain
epistemic strength. An important set of questions seem to be how the
agent has to behave in order to gain the epistemic strength that he
has. To make epistemic logic pertinent to epistemology, computer science,
artificial intelligence and cognitive psychology the activity of agents must be
included in our formal considerations. The original symbolic notation of a
knowing agent also suggests this: An agent term should be inside the scope of
the knowledge operator — not outside as Hintikka notes (1998). Inquiring agents
are agents who read data, change their minds, interact or have common knowledge,
act according to strategies and play games, have memory and act upon it, follow
various methodological rules, expand, contract or revise their knowledge bases,
etc. all in the pursuit of knowledge. Inquiring agents are active
agents (Hendricks 2003).
Game theory is about strategies for winning games in the context of other
agents. Game theory has therefore played a prominent role in reflections on
epistemic agency (the study of the behavior of interactive epistemic agents).
Aumann, van Benthem, Brandenburger, Fagin, Halpern, Keisler, Moses, Stalnaker,
Vardi and others have demonstrated how logical epistemology uncovers important
features of agent rationality showing how game theory adds to the
general understanding of notions like knowledge, belief and belief
revision.[1] Baltag, Moss, Solecki combine epistemic logic with
belief revision theory to study actions and belief updates in games (Baltag
et al. 1999).
Mixing the theory of belief change and epistemic logic furnishes an
illustrative example of active agents. The idea dates back to the mid 1990s.
Alchourrón, Gärdenfors and Makinson's seminal belief revision theory (AGM) from
the 1980s is a theory about the rational change of beliefs for expansions,
contractions and revisions in light of new (possibly conflicting) evidence
(Alchourrón 1985, Gärdenfors 1988). In 1994, de Rijke showed that the AGM-axioms
governing expansion and revision may be translated into the object language of
dynamic modal logic (de Rijke 1994). At about the same time, Segerberg
demonstrated how the entire theory of belief revision could be formulated in
modal logic.
Segerberg merged the static first generation doxastic logic with the dynamics
of belief change into ‘dynamic doxastic logic’ (Segerberg 1995). Doxastic
operators in the logic of belief like BcA
may be captured by AGM in the sense that ‘A is in c's
belief-set T’, or ¬Bc¬A becomes
‘¬A is not in c's belief-set T’. Similarly for other
combinations of the belief operator with negation. An immediate difference
between the two perspectives is that while AGM can express dynamic operations on
belief-sets like expansions (‘A is in c's belief-set
T expanded by D’, i.e., A ∈ T+D),
revisions (‘A is in c's belief-set T revised by
D’, i.e., A ∈ T*D), and contractions
(‘A is in c's belief-set T contracted by D’,
i.e. A ∈ T−D), no such dynamics are immediately
expressible in the standard language of doxastic logic. On the other hand,
action languages include operators like [ν] and <ν> which are prefixed to
a well-formed formula A. On Segerberg's interpretation, [ν]A
(<ν>A) mean that ‘after every (some) way of performing action ν
it is the case that A’. By introducing three new operators [+], [*],
and [−] into the doxastic language, the three dynamic operations on belief-sets
may be rendered as [+D]BcA,
[*D]BcA and
[−D]BcA.
After revising the original belief revision theory such that changes of
beliefs happen in ‘hypertheories’ or concentric spheres enumerated according to
entrencement Segerberg (1999a, 199b) has provided several axiomatizations of the
dynamic doxastic logic together with soundness and completeness results. The
dynamic doxastic logic paradigm may also be extended to iterated belief revision
as studied by Lindstrøm and Rabinowicz (1997) and accommodate various forms of
agent introspection. A related approach drawn up by van Ditmarsch, van der Hoek
and Kooi's new ‘dynamic epistemic logic’ studies how information changes and how
actions with epistemic impact on agents may be modelled (Hoek et al.
2003, Ditmarsch et al. 2006).
Active agenthood is also realizable directly on the agent level. One may also
choose to endow the agents with epistemic capacities facilitating
special epistemic behaviors. Fagin, Halpern, Moses and Vardi have for instance
considered ‘perfect recall’ (Fagin et al. 1995): interacting agents'
knowledge in the dynamic system may increase as time goes by but the agents may
still store old information. The agent's current local state is an encoding of
all events that have happened so far in the run. Perfect recall is in turn an
epistemic recommendation telling the agent to remember his earlier epistemic
states.
There are other structural properties of agents being studied in the
literature of dynamic epistemic logics. In an epistemic logic suited for
modeling various games of imperfect information van Benthem refers to such
properties as ‘styles of playing’ (van Benthem 2000). Properties like ‘bounded
memory’, various ‘mechanisms for information updates’ and ‘uniform strategies’,
infallibility, consistency etc. have been investigated. Agents as explcitly
learning mechanims are also integral parts of Kelly's (1996) computational
epistemology and a related approach called modal operator epistemology
(Hendricks 2001, 2003).
Researchers in artificial intelligence have additionally been trying to
describe and specify the behaviour of intelligent/rational agents by extensions
of epistemic of logic by augmenting logics of time, action and belief with
modalities for desires and intentions (see Meyer 2003), in particular, his
discussion of the BDI-framework of Rao and Georgeff in Section 5.2).
When epistemic logic was still in its infancy, Dana Scott noted:
Here is what I consider one of the biggest mistakes of all in
modal logic: concentration on a system with just one modal operator. The only
way to have any philosophically significant results in deontic logic or
epistemic logic is to combine these operators with: Tense operators (otherwise
how can you formulate principles of change?); the logical operators (otherwise
how can you compare the relative with the absolute?); the operators like
historical or physical necessity (otherwise how can you relate the agent to
his environment?); and so on and so on. (Scott 1970, 143)
Nowadays, there are various ways in which multi-modalities may be realized in
epistemic logic. One standard way is to follow Fagin et al. (1995). in
reinterpreting agents and possible worlds relative to systems of agents.[2]
In a system of agents each individual agent is considered to be in some
‘local state’. The whole system — as the sum of the local agents and other
envrionmental features — is accordingly in some `global state'. The dynamics may
be modeled by defining what is referred to as a ‘run’ over the system which is a
function from time to global states. The run may be construed as an account of
the behavior of the system for possible executions. Pairs of runs and times give
rise to `points'. For every time, the system is in some global state as a
function of the particular time. The system may be thought of as a series of
runs rather than agents. In this case, what is being modeled are the possible
behaviors of the system over a collection of executions. A system of this kind
defines a Kripke-structure with an equivalence relation over points. The
accessibility relation is specified with respect to possible points such that
some point w′ is accessible from the current point w if the
agent is in the same local state at w and w′. Knowledge is
defined with respect to the agents' local state. Truth of a formula is given
with respect to a point. If truth is relative to a point then there is a
question of when which opens up for the introduction of temporal
operators. One may for instance define a universal future-tense operator such
that a formula is true relative to the current point and all later points. The
mixture of epistemic and temporal operators can handle claims about the temporal
development of knowledge in the system.
Generally speaking, contemporary epistemology is organized around two major
goals: (1) The long-standing goal of providing a definition of knowledge and
simultaneously responding to the challenge of skepticism, and (2) The goal of
modeling the dynamics of epistemic and doxastic states. The first of these goals
has, for the most part, been a concern of philosophers who rely on thought
experiments, traditional conceptual analysis or intuitions-based methods of
various kinds. By contrast, philosophers working with epistemic logic have
pursued the second goal. The apparent divergence of both enterprises can be
reconciled to some extent once one recognizes that both goals relate to a third,
and possibly more general problem, namely (3) the problem of understanding the
rationality of inquiry. This problem is of equal importance to both epistemic
logicians and traditional epistemologists. Dynamical treatments of epistemic
logic and insights into the logic of inquiry from epistemic logicians speak
directly to this third, unifying goal. In recent decades, it is precisely the
dynamical model of knowledge and inquiry that has concerned
philosophically-inclined epistemic logicians. For a systematic treatment of the
interplay between epistemology and epistemic logic we refer to Hendricks and
Symons 2006.
Monographs and Anthologies
- Boh, I. (1993). Epistemic Logic in the Middle Ages. Routledge.
- van Ditmarsch, H., van der Hoek, W., and Kooi, P. (2006). Concurrent
Dynamic Epistemic Logic. Synthese Library Series. Dordrecht: Springer
- Gabbay, D. and Guenthner F. (1984). Handbook of Philosophical
Logic, vol. II: Extensions of Classical Logic. Dordrecht: D.
Reidel Publishing Company.
- Gärdenfors, P. (1988). Knowledge in Flux — Modelling the Dynamics of
Epistemic States. Cambridge: MIT Press.
- Fagin, R., Halpern, J. Y., Moses Y. and Vardi, M. Y. (1995). Reasoning
about Knowledge. Cambridge: MIT Press.
- Halpern, J.Y. (2003). Reasoning about Uncertainty. Cambridge: MIT
Press.
- Hansson, S.O. (1999). A Textbook on Belief Revision. Dordrecht:
Kluwer Academic Publishers
- Hendricks, V. F. (2001). The Convergence of Scientific Knowledge--a
view from the limit. Trends in Logic: Studia Logica Library Series,
Dordrecht: Kluwer Academic Publishers.
- Hendricks, V.F., Jørgensen, K.F, and Pedersen, S.A. (eds.) (2003).
Knowledge Contributors. Synthese Library, vol. 322. Dordrecht: Kluwer
Academic Publishers.
- Hendricks, V. F. (2005). Mainstream and Formal Epistemology. New
York: Cambridge University Press.
- Hendricks, V.F. and Pritchard, D. (eds.) (2006). New Waves in
Epistemology. Aldershot: Ashgate.
- Meyer, J.-J.Ch and Hoek, W. van der (1995). Epistemic Logic for AI and
Computer Science. Cambridge Tracts in Theoretical Computer Science 41.
Cambridge: Cambridge University Press.
- Hintikka, J. (1962). Knowledge and Belief: An Introduction to the
Logic of the Two Notions. Cornell: Cornell University Press.
- Kelly, K. (1996). The Logic of Reliable Inquiry. New York: Oxford
University Press.
- Knuuttila, S. (1993). Modal Logic in the Middle Ages. London:
Routledge.
- Kutschera, F. von. (1976). Einführung in die intensional
Semantik. Berlin: W. de Gruyter.
- Lemmon, E. J. (1977). An Introduction to Modal Logic, in
collaboration with D. Scott. Oxford: Basil Blackwell Publishers.
- Lenzen, W. (1978). Recent Work in Epistemic Logic, in Acta
Philosophica Fennica, 30: 1-219.
- Lewis, D. (1969). Convention, Cambridge MA: Harvard University
Press.
- Rescher, N. (2005). Epistemic Logic: Survey of the Logic of
Knowledge. Pittsburgh: University of Pittsburgh Press.
- Schlesinger, G.N. (1985). The Range of Epistemic Logic. Aberdeen:
Aberdeen University Press.
- Sowa, John F. (2000). Knowledge Representation: Logical,
Philosophical, and Computational Foundations. Pacific Grove, California:
Brooks/Cole.
- Von Wright, G., H. (1951). An Essay on Modal Logic. Amsterdam:
North-Holland Publishing Company.
- Voorbraak, F. (1993). As Far as I Know. Published as volume 7 in
Queastiones Infinitae. Department of Philosophy, Utrecht University.
Encyclopedia Articles
- Gochet, P. and Gribomont, P. (2003). ‘Epistemic Logic,’ forthcoming in
Handbook of the History and Philosophy of Logic, edited by Gabbay,
D.M. and Woods, J. Amsterdam: Elsevier Science.
- Hintikka, J. and Halonen, I. (1998). ‘Epistemic Logic’, Routledge
Encyclopedia of Philosophy, volume 1. London: Routledge: 752-3.
- Meyer, J.-J. Ch. (2001). ‘Epistemic Logic,’ chapter 9 of The Blackwell
Guide to Philosophical Logic (L. Goble, ed.), Oxford: Blackwell
Publishers: 183-200.
Papers
- Alchourrón, C.E., Gärdenfors, P. and Makinson, D. (1985). ‘On the Logic of
Theory Change, Journal of Symbolic Logic, 50: 510-530.
- Arlo Costa, H. (2006). ‘ Rationality and Value: The Epistemological Role
of Indeterminate and Agent-Dependent Values Philosophical Studies 127
3: 1-52
- Aumann, R.J. (1999a). ‘ Interactive Epistemology I: Knowledge,’
International Journal of Game Theory 28: 263-300
- Baltag, A., Moss, L.S., Solecki, S. (2002). ‘The Logic of Public
Annoucements, Common Knowledge, and Private Suspicion’. Proceedings of
TARK 1998. Los Altos: Morgan Kaufmann Publishers, 43-56
- Benthem, J.F.A.K. v. (2000). ‘Logic and Game Theory--close encounters of
the third kind’, in Prooceedings of LLC99, Loon, I.v., Mints, G. and
Muskens, R. (eds). Stanford: CSLI Publications.
- Benthem, J.F.A.K. v. (2003). ‘Logic Games are Complete for Game Logics’,
Studia Logica, 75(2): 183-203.
- Benthem, J.F.A.K. v. (2003). ‘Fifty Years: Changes and Constants in
Logic’, in Trends in Logic: 50 Years of Studia Logica. Edited by
Hendricks, V.F. and Malinowski, J., Dordrecht: Kluwer Academic Publishers:
35-56.
- Bull, R. and Segerberg, K. (1984). ‘Basic Modal Logic’, in Gabbay 1984,
1-88.
- Halpern, J. Y. (1995). ‘Should Knowledge Entail Belief?’, Journal of
Philosophical Logic, 25: 483-494.
- Hintikka, J. (1975). ‘Impossible Possible Worlds Vindicated’, Journal
of Philosophical Logic, 4: 475-484.
- Hendricks, V. F. (2003). ‘Active Agents’, Journal of Logic, Language
and Information, van Benthem, J. and van Rooy, R. (eds.). 12, 4: 469-495.
- Hendricks, V. F. and Symons J.(2006). ‘Where's the Bridge? Epistemic Logic
and Epistemology’, Philosophical Studies, 128, 1: 2-26.
- Hoek, W.v.d., Ditmarsch, H., Kooi, B. (2003). ‘Concurrent Dynamic
Epistemic Logic,’ in Hendricks 2005, 105-173.
- Hoek, W. van der, (1996). ‘Systems for Knowledge and Belief’, Journal
of Logic and Computation, 3: 173-195.
- Kripke, S. (1963). ‘Semantical Analysis of Modal Logic’, Zeitschrift
für Matematische Logik und Grundlagen der Matematik, 9: 67-96.
- Lindström, S. and Rabinowicz, W. (1997). ‘Extending Dynamic Logic:
Accommodating Iterated Beliefs and Ramsey Conditionals within DLL’, in For
Good Measure, Lindahl, L., Needham, P. and Sliwinski, R. (eds.).
Uppsala Philosophical Studies, 46: 123-153.
- Lindström, S. and Rabinowicz, W. (1999). ‘DDL Unlimited: Dynamic Doxastic
Logic for Introspective Agents’, Erkenntnis, 50: 353-385.
- Meyer, J.-J. Ch. (2003). ‘Modal Epistemic and Doxastic Logic,’ in:
Handbook of Philosophical Logic (2nd edition) (D. Gabbay & F.
Guenthner, eds.) Vol. 10, Dordrecht: Kluwer, 1-38.
- Rantala, V. (1975). ‘Urn Models: A New Kind of Non-Standard Model for
First-Order Logic’, Journal of Symbolic Logic, 4: 455-474.
- de Rijke, M. (1994). ‘Meeting Some Neighbours: A Dynamic Modal Logic Meets
Theories of Change and Knowledge Representation’, in Logic and Information
Flow, Eijck, J.v and Visser, A. (eds.). Cambridge: MIT Press, 170–196.
- Scott, D. (1970). ‘Advice on Modal Logic’, in Philosophical Problems
in Logic, Lambert, K. (ed.). Dordrecht: D. Reidel Publishing Company:
143-173.
- Segerberg, K. (1995). ‘Belief Revision from the Point of View of Doxastic
Logic’, Bulletin of the IGPL, 3: 535-553.
- Segerberg, K. (1999a). ‘The Basic Dynamic Doxastic Logic of AGM’,
Uppsala Prints and Preprints in Philosophy, 1.
- Segerberg, K. (1999b). ‘A Completeness Proof in Full DDL’, in
Philosophical Crumbs: Essays Dedicated to Ann-Mari Henschen-Dahlqvist on
the Occasion of her Seventyfifth Birthday, Sliwinski, R. (ed.).
Uppsala Philosophical Studies, 49: 195-207.
- Stalnaker, R. (1996). ‘Knowledge, Belief and Counterfactual Reasoning in
Games’, Economics and Philosophy, 12: 133-163.
common knowledge
| logic: modal
A | B | C | D | E | F | G | H | I | J | K | L | M | N | O | P | Q | R | S | T | U | V | W | X | Y | Z
Stanford Encyclopedia of Philosophy
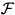 which in turn is a pair
<W,Rc> such that W is a
non-empty set of possible worlds and Rc is a binary
accessibility relation (relative to agent c) over W. A
model
which in turn is a pair
<W,Rc> such that W is a
non-empty set of possible worlds and Rc is a binary
accessibility relation (relative to agent c) over W. A
model 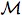 for an
epistemic system consists of a frame and a denotation function φ assigning sets
of worlds to atomic propositional formulas. Propositions are taken to be sets of
possible worlds; namely the set of possible worlds in which they are true. Let
atom be the set of atomic propositional formulae, then
φ : atom
for an
epistemic system consists of a frame and a denotation function φ assigning sets
of worlds to atomic propositional formulas. Propositions are taken to be sets of
possible worlds; namely the set of possible worlds in which they are true. Let
atom be the set of atomic propositional formulae, then
φ : atom 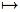 P(W), where P denotes the powerset operation. The
model
P(W), where P denotes the powerset operation. The
model 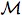 =
<W,Rc,φ> is called a Kripke-model
and the resulting semantics Kripke-semantics (Kripke 1963): An atomic
propositional formula, a, is said to be true in a world
w in
=
<W,Rc,φ> is called a Kripke-model
and the resulting semantics Kripke-semantics (Kripke 1963): An atomic
propositional formula, a, is said to be true in a world
w in 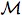 (written
(written 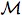 ,w
,w 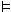 a) iff w is in
the set of possible worlds assigned to a, i.e.,
a) iff w is in
the set of possible worlds assigned to a, i.e., 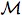 ,w
,w 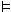 a iff w ∈
φ(a) for all a ∈ atom . The formula
KcA is true in an world w (i.e.,
a iff w ∈
φ(a) for all a ∈ atom . The formula
KcA is true in an world w (i.e.,
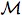 ,w
,w 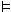 KcA) iff ∀w′∈W, if
Rcww′, then
KcA) iff ∀w′∈W, if
Rcww′, then 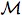 ,w′
,w′ 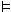 A. The semantics for the
Boolean connectives follow the usual recursive recipe. A modal formula is said
to be valid in a frame iff the formula is true for all possible
assignments in all worlds in the frame.
A. The semantics for the
Boolean connectives follow the usual recursive recipe. A modal formula is said
to be valid in a frame iff the formula is true for all possible
assignments in all worlds in the frame.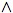 Rw′w″ → Rww″ then the axiom reflecting the idea that
the agent knows that he knows A if he does,
Rw′w″ → Rww″ then the axiom reflecting the idea that
the agent knows that he knows A if he does,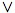 Kc(KcA′
→ KcA)
Kc(KcA′
→ KcA)