version history
|
A | B | C | D | E | F | G | H | I | J | K | L | M | N | O | P | Q | R | S | T | U | V | W | X | Y | Z
| This document uses XHTML/Unicode to
format the display. If you think special symbols are not displaying
correctly, see our guide Displaying
Special Characters. | |
last substantive content
change
|
Provability logic
Provability logic is a modal logic that is used to investigate what
arithmetical theories can express in a restricted language about their
provability predicates. The logic has been inspired by developments in
meta-mathematics such as Gödel's incompleteness theorems of 1931 and Löb's
theorem of 1953. As a modal logic, provability logic has been studied since the
early seventies, and has had important applications in the foundations of
mathematics.
From a philosophical point of view, provability logic is interesting because
the concept of provability in a fixed theory of arithmetic has a unique and
non-problematic meaning, other than concepts like necessity and knowledge
studied in modal and epistemic logic. Furthermore, provability logic provides
tools to study the notion of self-reference.
Two strands of research have led to the birth of provability logic. The first
one stems from a paper by K. Gödel (1933), where he introduces a translation
from intuitionistic propositional logic into modal logic (more precisely, into
the system nowadays called S4), and briefly mentions that provability can be
viewed as a modal operator. Even earlier, C.I. Lewis started the modern study of
modal logic by introducing strict implication as a kind of deducibility, where
he may have meant deducibility in a formal system like Principia Mathematica,
but this is not clear from his writings.
The other strand starts from research in meta-mathematics: what can
mathematical theories say about themselves by encoding interesting properties?
In 1952, L. Henkin posed a deceptively simple question inspired by Gödel's
incompleteness theorems. In order to formulate Henkin's question, some more
background is needed. As a reminder, Gödel's first incompleteness theorem states
that, for a sufficiently strong formal theory like Peano Arithmetic, any
sentence asserting its own unprovability is in fact unprovable. On the other
hand, from "outside" the formal theory, one can see that such a sentence is true
in the standard model, pointing to an important distinction between truth and
provability.
More formally, let  A
A denote the Gödel number of
arithmetical formula A, the result of assigning a numerical code to
A. Let Prov be the formalized provability predicate for Peano
Arithmetic, which is of the form
denote the Gödel number of
arithmetical formula A, the result of assigning a numerical code to
A. Let Prov be the formalized provability predicate for Peano
Arithmetic, which is of the form 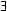 p Proof
(p,x). Here, Proof is the formalized proof predicate
of Peano Arithmetic, and Proof(p,x) stands for Gödel
number p codes a correct proof from the axioms of Peano Arithmetic of
the formula with Gödel number x. (For a more precise formulation, see
Smorynski (1985), Davis (1958)). Now, suppose that Peano Arithmetic proves
A
p Proof
(p,x). Here, Proof is the formalized proof predicate
of Peano Arithmetic, and Proof(p,x) stands for Gödel
number p codes a correct proof from the axioms of Peano Arithmetic of
the formula with Gödel number x. (For a more precise formulation, see
Smorynski (1985), Davis (1958)). Now, suppose that Peano Arithmetic proves
A 
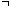 Prov
Prov A
A , then by Gödel's result,
A is not provable in Peano Arithmetic, and thus it is true, for in fact
the self-referential sentence A states “I am not provable”.
, then by Gödel's result,
A is not provable in Peano Arithmetic, and thus it is true, for in fact
the self-referential sentence A states “I am not provable”.
Henkin on the other hand wanted to know whether anything could be said about
sentences asserting their own provability: supposing that Peano Arithmetic
proves B  Prov(
Prov( B
B ), what does this imply about
B? Three years later, M. Löb took up the challenge and answered
Henkin's question in a surprising way. Even though all sentences provable in
Peano Arithmetic are indeed true about the natural numbers, Löb showed that the
formalized version of this fact, Prov(
), what does this imply about
B? Three years later, M. Löb took up the challenge and answered
Henkin's question in a surprising way. Even though all sentences provable in
Peano Arithmetic are indeed true about the natural numbers, Löb showed that the
formalized version of this fact, Prov( B
B )
)  B, can only be proved in Peano
Arithmetic in the trivial case that Peano Arithmetic already proves B
itself. This result, now called Löb's theorem, immediately answers Henkin's
question. (For a proof of Löb's theorem, see section 4.)
Löb also showed a formalized version of his theorem, namely that Peano
Arithmetic proves
B, can only be proved in Peano
Arithmetic in the trivial case that Peano Arithmetic already proves B
itself. This result, now called Löb's theorem, immediately answers Henkin's
question. (For a proof of Löb's theorem, see section 4.)
Löb also showed a formalized version of his theorem, namely that Peano
Arithmetic proves
Prov( Prov(
Prov( B
B )
)  B
B )
) Prov(
Prov( B
B ).
).
In the same paper, Löb formulated three conditions on the provability
predicate of Peano Arithmetic, that form a useful modification of the
complicated conditions that Hilbert and Bernays introduced in 1939 for their
proof of Gödel's second incompleteness theorem. In the following, derivability
of A from Peano Arithmetic is denoted by PA A:
A:
- If PA
 A, then PA
A, then PA Prov(
Prov( A
A );
);
- PA
 Prov(
Prov( A
A B
B )
)  (Prov(
(Prov( A
A )
)  Prov(
Prov( B
B ));
));
- PA
 Prov(
Prov( A
A )
)  Prov(
Prov( Prov(
Prov( A
A )
) ).
).
These Löb conditions, as they are called nowadays, seem to cry out for a
modal logical investigation, where the modality  stands for provability in PA. Ironically,
the first time that the formalized version of Löb's theorem was stated as the
modal principle
stands for provability in PA. Ironically,
the first time that the formalized version of Löb's theorem was stated as the
modal principle
 (
( A
A  A)
A) 
 A
A
was in a paper by
Smiley in 1963 about the logical basis of ethics, which did not consider
arithmetic at all. More relevant investigations, however, only seriously started
almost twenty years after publication of Löb's paper. The early seventies saw
the rapid development of propositional provability logic, where several
researchers in different countries independently proved the most important
results, discussed in sections 2, 3, and 4.
Propositional provability logic turned out to capture exactly what many formal
theories of arithmetic can say by propositional means about their own
provability predicate. Recently, researchers have investigated the boundaries of
this approach and have proposed several interesting more expressive extensions
of provability logic (see section 5).
The logical language of propositional provability logic contains, in addition
to propositional atoms and the usual truth-functional operators as well as the
contradiction symbol 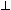 , a modal
operator
, a modal
operator  with intended meaning “is
provable in T,” where T is a sufficiently strong formal
theory, let us say Peano Arithmetic (see section 4).
with intended meaning “is
provable in T,” where T is a sufficiently strong formal
theory, let us say Peano Arithmetic (see section 4).
 A is an abbreviation
for
A is an abbreviation
for 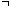

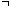 A. Thus, the language is the
same as that of modal systems such as K and S4 presented in the entry modal logic.
A. Thus, the language is the
same as that of modal systems such as K and S4 presented in the entry modal logic.
Propositional provability logic is often called GL, after Gödel and Löb.
(Alternative names found in the literature for equivalent systems are L, KW,
K4W, and PrL). The logic GL results from adding the following axiom to the basic
modal logic K:
(GL)  (
( A
A  A)
A) 
 A.
A.
As a reminder,
because GL extends K, it contains all formulas having the form of a
propositional tautology. For the same reason, GL contains the
Distribution Axiom:  (A
(A B)
B)  (
( A
A
 B).
B).
Furthermore, it
is closed under the Modus Ponens Rule allowing to derive B from
A  B and B,
and the Generalization Rule, which says that if A is a theorem of GL,
then so is
B and B,
and the Generalization Rule, which says that if A is a theorem of GL,
then so is  A.
A.
The notion GL  A
denotes provability of a modal formula A in propositional provability
logic. It is not difficult to see that the modal axiom
A
denotes provability of a modal formula A in propositional provability
logic. It is not difficult to see that the modal axiom  A
A

 A (known as axiom 4 of modal
logic) is indeed provable in GL. To prove this, one uses the substitution
A
A (known as axiom 4 of modal
logic) is indeed provable in GL. To prove this, one uses the substitution
A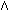
 A for A in the axiom
(GL), and applies the Distribution Axiom and the Generalization Rule as well as
some propositional logic. Unless explicitly stated otherwise, in the sequel
“provability logic” stands for the system GL of propositional provability
logic.
A for A in the axiom
(GL), and applies the Distribution Axiom and the Generalization Rule as well as
some propositional logic. Unless explicitly stated otherwise, in the sequel
“provability logic” stands for the system GL of propositional provability
logic.
The main "modal" result
about provability logic is the fixed point theorem, which D. de Jongh and G.
Sambin independently proved in 1975. Even though it is formulated and proved by
strictly modal methods, the fixed point theorem still has great arithmetical
significance. It says essentially that self-reference is not really necessary,
in the following sense. Suppose that all occurrences of the propositional
variable p in a given formula A(p) are under the
scope of the provability operator, for example A(p) = 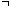
 p, or A(p) =
p, or A(p) =
 (p
(p  q). Then there is a formula
B in which p does not appear, such that all propositional
variables that occur in B already appear in A(p), and
such that
q). Then there is a formula
B in which p does not appear, such that all propositional
variables that occur in B already appear in A(p), and
such that
GL  B
B  A(B).
A(B).
This
formula B is called a fixed point of A(p).
Moreover, the fixed point is unique, or more accurately, if there is another
formula C such that GL  C
C  A(C),
then we must have GL
A(C),
then we must have GL  B
B C. Most proofs in
the literature give an algorithm by which one can compute the fixed point (see
Smorynski 1985, Boolos 1993).
C. Most proofs in
the literature give an algorithm by which one can compute the fixed point (see
Smorynski 1985, Boolos 1993).
For example, suppose that A(p) = 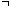
 p. Then the fixed point produced
by such an algorithm is
p. Then the fixed point produced
by such an algorithm is 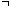

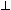 , and indeed one can prove that
, and indeed one can prove that
GL 
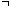

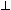

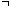
 (
(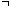

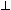 ).
).
If this is read
arithmetically, the direction from left to right is just the formalized version
of Gödel's second incompleteness theorem: if a sufficiently strong formal theory
T like Peano Arithmetic does not prove a contradiction, then it is not
provable in T that T does not prove a contradiction. Thus,
sufficiently strong consistent arithmetical theories cannot prove their own
consistency. We will turn to study the relation between provability logic and
arithmetic more precisely in section 4, but
to that end another “modal” aspect of GL needs to be provided first: semantics.
Provability logic has suitable possible worlds semantics, just like many
other modal logics. As a reminder, a possible worlds model (or Kripke model) is
a triple M = 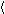 W,R,V
W,R,V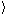 , where W is a set of
possible worlds, R is a binary accessibility relation on W,
and V is a valuation that assigns a truth value to each propositional
variable for each world in W. The pair F =
, where W is a set of
possible worlds, R is a binary accessibility relation on W,
and V is a valuation that assigns a truth value to each propositional
variable for each world in W. The pair F = 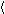 W,R
W,R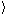 is called the frame of this model.
The notion of truth of a formula A in a model M at a world
W, notation M,w
is called the frame of this model.
The notion of truth of a formula A in a model M at a world
W, notation M,w 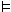 A, is defined inductively.
Let us repeat only the most interesting clause, the one for the provability
operator
A, is defined inductively.
Let us repeat only the most interesting clause, the one for the provability
operator  :
:
M,w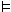
 A iff for every w
A iff for every w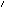 , if wRw
, if wRw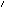 , then M,w
, then M,w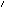
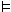 A.
A.
See the entry
modal logic for more information about possible worlds semantics in
general.
The modal logic K is valid in all Kripke models. Its extension GL however, is
not: we need to restrict the class of possible worlds models to a more suitable
one. Let us say that a formula A is valid in frame F, notation
F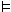 A, iff
A is true in all worlds in Kripke models M based on
F. It turns our that the new axiom (GL) of provability logic
corresponds to a condition on frames, as follows:
A, iff
A is true in all worlds in Kripke models M based on
F. It turns our that the new axiom (GL) of provability logic
corresponds to a condition on frames, as follows:
For all frames F = <W,R>,
F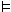
 (
( p
p p)
p) 
 p iff R is transitive
and conversely well-founded.
p iff R is transitive
and conversely well-founded.
Here, transitivity is the well-known property that for all worlds
w1, w2, w3 in
W, if w1Rw2 and
w2Rw3, then
w1Rw3. A relation is conversely
well-founded iff there are no infinite ascending sequences, that is
sequences of the form
w1Rw2Rw3R….
Note that conversely well-founded frames are also irreflexive, for if wRw, this
gives rise to an infinite ascending sequence wRwRwR….
The above correspondence result immediately shows that GL is modally sound
with respect to the class of possible worlds models on transitive conversely
well-founded frames, because all axioms and rules of GL are valid on such
models. The question is whether completeness also holds: for example, the
formula  A
A

 A, which is valid on all
transitive frames, is indeed provable in GL, as was mentioned in Section 1. But
are all valid formulas provable in GL?
A, which is valid on all
transitive frames, is indeed provable in GL, as was mentioned in Section 1. But
are all valid formulas provable in GL?
Unaware of the arithmetical significance of GL, K. Segerberg proved in 1971
that GL is indeed complete with respect to transitive conversely well-founded
frames; D. de Jongh and S. Kripke independently proved this result as well.
Segerberg showed that GL is complete even with respect to the more restricted
class of finite transitive irreflexive trees, a fact which later turned out to
be very useful for Solovay's proof of the arithmetical completeness theorem (see
Section
4).
The modal soundness and completeness theorems immediately give rise to a
decision procedure to check for any modal formula A whether A
follows from GL or not. Looking at the procedure a bit more precisely, it can be
shown that GL is decidable in the computational complexity class PSPACE, like
the well-known modal logics K, T and S4. This means that there is a Turing
machine that, given a formula A as input, answers whether A
follows from GL or not; the size of the memory that the Turing machine needs for
its computation is only polynomial in the length of A.
To give some more perspective on complexity, the class P of functions
computable in an amount of time polynomial in the length of the input, is
included in PSPACE, which in turn is included in the class EXPTIME of functions
computable in exponential time. It remains a famous open problem whether these
two inclusions are strict, although many complexity theorists believe that they
are. Some other well-known modal logics, like epistemic logic with common
knowledge, are decidable in EXPTIME, thus they may be more complex than GL,
depending on the open problems.
Many well-known modal logics S are not only complete with respect to
an appropriate class of frames, but even strongly complete in the sense
that for all (finite or infinite) sets 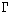 and all formulas A:
and all formulas A:
If, on appropriate S-frames, A is true in all
worlds in which all formulas of 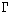 are true, then
are true, then 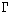
 A in the logic
S.
A in the logic
S.
This condition holds for systems like K, M, K4, S4, and
S5. If restricted to finite sets 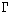 ,
the above condition corresponds to completeness.
,
the above condition corresponds to completeness.
Strong completeness does not hold for provability logic, however, because
semantic compactness fails. Semantic compactness is the property that
for each infinite set 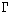 of formulas,
of formulas,
If every finite subset 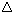 of
of 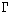 has a model on an appropriate
S-frame, then
has a model on an appropriate
S-frame, then 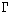 also has
a model on an appropriate S-frame.
also has
a model on an appropriate S-frame.
As a counterexample, take the infinite set of formulas
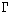 = {
= { p0,
p0,  (p0
(p0
 p1),
p1),  (p1
(p1
 p2),
p2),  (p2
(p2 
 p3),…,
p3),…,  (pn
(pn
 pn+1),…}
pn+1),…}
Then for every finite subset
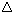 of
of 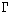 , one can construct a model on a
transitive, conversely well-founded frame and a world in the model where all
formulas of
, one can construct a model on a
transitive, conversely well-founded frame and a world in the model where all
formulas of 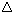 are true. So by modal
soundness, GL does not prove
are true. So by modal
soundness, GL does not prove 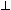 from
from
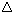 for any finite
for any finite 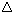
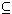
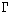 , and a fortiori GL does not
prove
, and a fortiori GL does not
prove 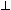 from
from 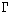 , as any GL-proof is finite. On the
other hand, it is easy to see that there is no model on a transitive, conversely
well-founded frame where in any world, all formulas of
, as any GL-proof is finite. On the
other hand, it is easy to see that there is no model on a transitive, conversely
well-founded frame where in any world, all formulas of 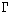 hold. Thus
hold. Thus 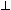 follows semantically from
follows semantically from 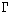 , but is not provable from it in GL,
contradicting the condition of strong completeness.
, but is not provable from it in GL,
contradicting the condition of strong completeness.
From the time GL was formulated, researchers wondered whether it was adequate
for formal theories like Peano Arithmetic (PA): does GL prove
everything about the notion of provability that can be expressed in a
propositional modal language and can be proved in Peano Arithmetic, or should
more principles be added to GL? To make this notion of adequacy more precise, we
define a realization (sometimes called translation or interpretation)
to be a function f that assigns to each propositional atom of modal logic a
sentence of arithmetic, where
- f(
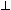 )=
)=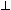 ;
;
- f respects the logical connectives (for example,
f(B
 C) =
(f(B)
C) =
(f(B) f(C)); and
f(C)); and
 is translated as the
provability predicate Prov, so f(
is translated as the
provability predicate Prov, so f( B) = Prov (
B) = Prov ( f(B)
f(B) ).
).
It was already clear in the early seventies that GL is arithmetically
sound with respect to PA, formally:
If GL  A,
then for all realizations f, PA
A,
then for all realizations f, PA  f(A).
f(A).
To
give some taste of meta-mathematics, let us sketch the soundness proof.
Proof sketch of arithmetical soundness
PA indeed proves
realizations of propositional tautologies, and provability of the Distribution
Axiom of GL translates to
PA Prov(
Prov( A
A B
B )
)  (Prov(
(Prov( A
A )
)  Prov(
Prov( B
B ))
))
for all
formulas A and B, which is just Löb's second derivability
condition (see Section 1).
Moreover, PA obeys Modus Ponens, as well as the translation of the
Generalization Rule:
If PA A,
then PA
A,
then PA Prov(
Prov( A
A ),
),
which is just
Löb's first derivability condition. Finally, the translation of the main axiom
(GL) is indeed provable in PA:
PA Prov(
Prov( Prov(
Prov( A
A )
)  A
A )
)  Prov(
Prov( A
A ).
).
This is exactly
the formalized version of Löb's theorem mentioned in Section 1 .
Let us give a sketch of the proof of Löb's theorem itself from his
derivability conditions (the proof of the formalized version is similar). The
proof is based on Gödel's Diagonalization lemma, which says that for any
arithmetical formula C(x) there is an arithmetical formula
B such that
PA B
B  C(
C( B
B ).
).
In words, the
formula B says “I have property C.”
Proof of Löb's theorem:
Suppose that PA Prov(
Prov( A
A )
) A, we need to show that PA
A, we need to show that PA A. By the Diagonalization
lemma, there is a formula B such that
A. By the Diagonalization
lemma, there is a formula B such that
PA B
B (Prov(
(Prov( B
B )
) A).
A).
From this it
follows by Löb's first and second derivability conditions plus some
propositional reasoning that
PA Prov(
Prov( B
B )
)  Prov(
Prov( Prov (
Prov ( B
B )
)  A
A ).
).
Thus, again by
Löb's second condition,
PA Prov(
Prov( B
B )
)  (Prov(
(Prov( Prov(
Prov( B
B )
)  )
) Prov(
Prov( A
A )).
)).
On the other
hand Löb's third condition gives
PA Prov(
Prov( B
B )
) Prov(
Prov( Prov(
Prov( B
B )
) ),
),
thus
PA Prov(
Prov( B
B )
) Prov(
Prov( A
A ).
).
Together with
the assumption that PA Prov(
Prov( A
A )
)  A, this gives
A, this gives
PA Prov(
Prov( B
B )
) A.
A.
Finally, the
equation produced by Diagonalization implies that PA B, so PA
B, so PA Prov(
Prov( B
B ), thus
), thus
PA A,
A,
as desired.
Note that substituting 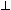 for
A in Löb's theorem, we derive that PA
for
A in Löb's theorem, we derive that PA
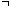 Prov (
Prov (
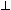
 ) implies PA
) implies PA
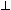 , which is just the contraposition of
Gödel's second incompleteness theorem.
, which is just the contraposition of
Gödel's second incompleteness theorem.
The landmark result in provability logic is R. Solovay's arithmetical
completeness theorem of 1976, showing that GL is indeed adequate for Peano
Arithmetic:
GL  A if
and only if for all realizations f, PA
A if
and only if for all realizations f, PA  f(A).
f(A).
This theorem says essentially that the modal logic GL captures
everything that Peano Arithmetic can say in modal terms about its own
provability predicate. The direction from left to right, arithmetical soundness
of GL, is discussed above. Solovay set out to prove the other, much more
difficult, direction by contraposition. His proof is based on intricate
self-referential techniques, and only a small glimpse can be given here.
The modal completeness theorem by Segerberg was an important first step in
Solovay's proof of arithmetical completeness of GL with respect to Peano
Arithmetic. Suppose that GL does not prove the modal formula A. Then,
by modal completeness, there is a finite transitive irreflexive tree such that
A is false at the root of that tree. Now Solovay devised an ingenious
way to simulate such a finite tree in the language of Peano Arithmetic. Thus he
found a realization f from modal formulas to sentences of arithmetic, such that
Peano Arithmetic does not prove f(A).
Solovay's completeness theorem provides an alternative way to construct many
arithmetical sentences that are not provable in Peano Arithmetic. For example,
it is easy to make a possible worlds model to show that GL does not prove  p
p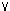

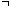 p, so by Solovay's theorem, there
is an arithmetical sentence f(p) such that Peano Arithmetic
does not prove Prov(
p, so by Solovay's theorem, there
is an arithmetical sentence f(p) such that Peano Arithmetic
does not prove Prov( f(p)
f(p) )
) 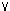 Prov(
Prov(
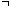 f(p)
f(p) ). In particular, this implies
that neither f(p) nor
). In particular, this implies
that neither f(p) nor 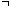 f(p) is provable in
Peano Arithmetic; for suppose on the contrary that PA
f(p) is provable in
Peano Arithmetic; for suppose on the contrary that PA  f(p), then by Löb's
first condition and propositional logic, PA
f(p), then by Löb's
first condition and propositional logic, PA  Prov(
Prov( f(p)
f(p) )
) 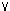 Prov(
Prov(
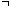 f(p)
f(p) ), leading to a contradiction,
and similarly if one supposes that PA
), leading to a contradiction,
and similarly if one supposes that PA 
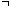 F(p).
F(p).
Solovay's theorem is so significant because it shows that an interesting
fragment of an undecidable formal theory like Peano Arithmetic -- namely that
which arithmetic can express in propositional terms about its own provability
predicate -- can be studied by means of a decidable modal logic, GL, with a
perspicuous possible worlds semantics.
In this section, some recent trends in research on provability logic are
discussed. One important strand concerns the limits on the scope of GL, where
the main question is, for which formal theories, other than Peano Arithmetic, is
GL the appropriate propositional provability logic? Next, we discuss some
generalizations of propositional provability logic in more expressive modal
languages.
In recent years, logicians have investigated many other systems of arithmetic
that are weaker than Peano Arithmetic. Often these logicians took their
inspiration from computability issues, for example the study of functions
computable in polynomial time. They have given a partial answer to the question:
“For which theories of arithmetic does Solovay's arithmetical completeness
theorem (with respect to the appropriate provability predicate) still hold?” To
discuss this question, two concepts are needed. 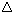 0-formulas are arithmetical
formulas in which all quantifiers are bounded by a term, for example
0-formulas are arithmetical
formulas in which all quantifiers are bounded by a term, for example
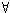 y
y 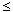 ss0
ss0 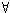 z
z 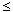 y
y 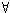 x
x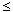 y+z
(x+y
y+z
(x+y 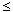 (y+(y+z))),
(y+(y+z))),
where s is
the successor operator (“+1”). The arithmetical theory I 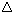 0 (where I stands for
"induction"), is similar to Peano Arithmetic, except that it allows less
induction: the induction scheme
0 (where I stands for
"induction"), is similar to Peano Arithmetic, except that it allows less
induction: the induction scheme
A(0) 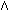
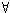 x(A(x)
x(A(x) A(sx))
A(sx)) 
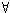 x A(x)
x A(x)
is restricted to 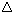 0-formulas A.
0-formulas A.
As De Jongh and others (1991) pointed out, arithmetical completeness
certainly holds for theories T that satisfy the following two
conditions:
- T proves induction for
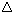 0-formulas, and T
proves EXP, the formula expressing that for all x, its power
2x exists. In more standard notation: T extends
I
0-formulas, and T
proves EXP, the formula expressing that for all x, its power
2x exists. In more standard notation: T extends
I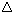 0+EXP;
0+EXP;
- T does not prove any false sentences of the form
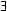 x A(x),
with A(x) a
x A(x),
with A(x) a 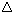 0-formula.
0-formula.
For such theories, arithmetical soundness and completeness of GL hold,
provided that  translates to
ProvT, a natural provability predicate with respect
to a sufficiently simple axiomatization of T. Thus for modal sentences
A:
translates to
ProvT, a natural provability predicate with respect
to a sufficiently simple axiomatization of T. Thus for modal sentences
A:
GL  A if
and only if for all realizations f, T
A if
and only if for all realizations f, T  f(A).
f(A).
It is not clear yet whether condition 1 gives a lower bound on the scope of
provability logic. For example, it is still an open question whether GL is the
provability logic of I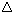 0+
0+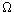 1, a theory which is somewhat
weaker than I
1, a theory which is somewhat
weaker than I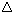 0+EXP in that
0+EXP in that 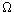 1 is the axiom asserting that
for all x, its power xlog(x) exists.
Provability logic GL is arithmetically sound with respect to I
1 is the axiom asserting that
for all x, its power xlog(x) exists.
Provability logic GL is arithmetically sound with respect to I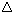 0+
0+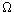 1, but except for some
partial results by Berarducci et al. (1993), providing arithmetic realizations
consistent with I
1, but except for some
partial results by Berarducci et al. (1993), providing arithmetic realizations
consistent with I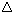 0 +
0 + 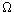 1 for a restricted class of
sentences consistent with GL, the question remains open. Its answer may hinge on
open problems in computational complexity theory.
1 for a restricted class of
sentences consistent with GL, the question remains open. Its answer may hinge on
open problems in computational complexity theory.
The above result by De Jongh et al. shows a strong feature of provability
logic: for many different arithmetical theories, GL captures exactly what those
theories say about their own provability predicates. At the same time this is a
weakness. For example, propositional provability logic does not point to any
differences between those theories that are finitely axiomatizable and those
that are not.
In order to be able to speak in a modal language about important distinctions
between theories, researchers have extended provability logic in many different
ways. Let us mention a few. One extension is to add a binary modality 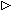 , where for a given arithmetical theory
T, the modal sentence A
, where for a given arithmetical theory
T, the modal sentence A 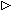 B is meant to stand for
“T+B is interpretable in T+A.” Visser
characterized the interpretability logic of the most common finitely axiomatized
theories, and Berarducci and Shavrukov independently characterized the one for
PA. It appears that indeed, the interpretability logic of finitely axiomatizable
theories is different from the interpretability logic of Peano Arithmetic, which
is not finitely axiomatizable (see Visser (1990,1997), Berarducci (1990),
Shavrukov (1988)).
B is meant to stand for
“T+B is interpretable in T+A.” Visser
characterized the interpretability logic of the most common finitely axiomatized
theories, and Berarducci and Shavrukov independently characterized the one for
PA. It appears that indeed, the interpretability logic of finitely axiomatizable
theories is different from the interpretability logic of Peano Arithmetic, which
is not finitely axiomatizable (see Visser (1990,1997), Berarducci (1990),
Shavrukov (1988)).
Another way to extend the framework of propositional provability logic is to
add propositional quantifiers, so that one can express principles like
Goldfarb's:
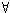 p
p 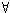 q
q 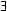 r
r  ((
(( p
p 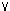
 q)
q) 
 r),
r),
saying that for
any two sentences there is a third sentence which is provable if and only if
either of the first two sentences is provable. This principle is provable in
Peano Arithmetic. The set of sentences of GL with propositional quantifiers that
is arithmetically valid turns out to be undecidable (Shavrukov (1997)).
Finally, one can of course study predicate provability logic. The language is
that of predicate logic without function symbols, together with the operator
 . Here, the situation becomes much
more complex than in the case of propositional provability logic. Is there a
nicely axiomatized predicate provability logic that is adequate, proving exactly
the valid principles of provability? The answer is unfortunately a resounding
no: Vardanyan (1986) has proved on the basis of ideas by Artëmov (1985) that the
set of sentences of predicate provability logic all of whose realizations are
provable in PA is not even recursively enumerable, so it has no reasonable
axiomatization.
. Here, the situation becomes much
more complex than in the case of propositional provability logic. Is there a
nicely axiomatized predicate provability logic that is adequate, proving exactly
the valid principles of provability? The answer is unfortunately a resounding
no: Vardanyan (1986) has proved on the basis of ideas by Artëmov (1985) that the
set of sentences of predicate provability logic all of whose realizations are
provable in PA is not even recursively enumerable, so it has no reasonable
axiomatization.
Left out in the above
discussion are many other important strands of research in provability logic and
its extensions. The interested reader is pointed to the following areas:
- the provability logic of intuitionistic arithmetic (see Troelstra (1973),
Visser (1994, 1999), Iemhoff (2000, 2001));
- Rosser orderings and proof speed-up (see Guaspari and Solovay (1979),
Svejdar (1983), Montagna (1992));
- classification of provability logics (see Visser (1980), Beklemishev et
al. (1999));
- the logic of explicit proofs (see Artëmov (2001));
- applications of provability logic in proof theory (see Beklemishev
(1999));
- bimodal provability logics with provability operators for different
theories (see Beklemishev (1994, 1996)); and
- provability algebras, also called diagonalizable algebras or Magari
algebras (see Shavrukov (1993, 1997)).
Even though propositional provability logic is a modal logic with a kind of
“necessity” operator, it withstands Quine's (1976) critique of modal notions as
unintelligible, because of its clear and unambiguous arithmetic interpretation.
For example, unlike for many other modal logics, formulas with nested modalities
like 
 p
p 

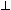 are not problematic, nor are there any
disputes about which ones should be tautologies. In fact, provability logic
embodies all the desiderata that Quine (1953) set out for syntactic treatments
of modality.
are not problematic, nor are there any
disputes about which ones should be tautologies. In fact, provability logic
embodies all the desiderata that Quine (1953) set out for syntactic treatments
of modality.
Quine's main arrows were pointed towards modal predicate logics, especially
the construction of sentences that contain modal operators under the scope of
quantifiers (“quantifying in”). In predicate provability logic, however, where
quantifiers range over natural numbers, both de dicto and de
re modalities have straightforward interpretations, contrary to the case of
other modal logics (see the note on the de
dicto / de re distinction). For example, formulas like
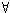 x
x 
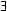 y (y = x)
y (y = x)
are not at all problematic. If the number n is assigned to
x, then 
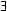 y (y = x) is
true with respect to this assignment iff the sentence
y (y = x) is
true with respect to this assignment iff the sentence 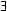 y (y =
In) is provable in Peano Arithmetic; here,
In is the numeral of n, i.e. the term
ss…s0 with n occurrences of the
successor operator s. This sentence is true for all
n in the standard model of the natural numbers, and
y (y =
In) is provable in Peano Arithmetic; here,
In is the numeral of n, i.e. the term
ss…s0 with n occurrences of the
successor operator s. This sentence is true for all
n in the standard model of the natural numbers, and 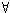 x
x 
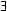 y (y = x) is
even provable in Peano Arithmetic.
y (y = x) is
even provable in Peano Arithmetic.
By the way, the Barcan Formula
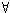 x
x  A(x)
A(x)

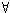 x A(x)
x A(x)
is not true for the integers, let alone provable (for example, take
for A(x) the formula “x does not code a proof of 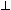 ”). Its converse
”). Its converse

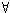 xA(x)
xA(x) 
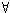 x
x A(x),
A(x),
on
the other hand, is provable in Peano Arithmetic for any formula A.
Provability logic has very different principles from other modal logics, even
those with a seemingly similar purpose. For example, while provability logic
captures provability in formal theories of arithmetic, epistemic logic endeavors
to describe knowledge, which could be viewed as a kind of informal provability.
In many versions of epistemic logic, one of the most important principles is the
truth axiom (5):
S5 
 A
A A, (if one knows A,
then A is true).
A, (if one knows A,
then A is true).
The analogous principle clearly does not
hold for GL: after all,
if GL
 A
A A, then GL
A, then GL A.
A.
Thus, it
seems misguided to compare the strength of both notions or to combine them in
one modal system. Perhaps formal provability is indeed in some sense a stronger
notion than informal provability, but definitely this is not an arithmetic truth
or validity, nor is the other direction. Discussions of the consequences of
Gödel's incompleteness theorems sometimes involve confusion around the notion of
provability, giving rise to claims that humans could beat formal systems in
“knowing” theorems (see Davis (1990, 1993) for good discussions of such claims).
All in all, formal provability is a precisely defined concept, much more so
than truth and knowledge. Thus, self-reference within the scope of provability
does not lead to semantic paradoxes like the Liar. Instead, it has led to some
of the most important results about mathematics, such as Gödel's incompleteness
theorems.
General references on provability logic
- Boolos, G.,The Unprovability of Consistency: An Essay in Modal
Logic, Cambridge, Cambridge University Press (1979).
- Boolos, G.,The Logic of Provability, New York and Cambridge:
Cambridge University Press (1993).
- Jongh, D.H.J. de and Japaridze, G., “The Logic of Provability,” in Buss,
S.R. (ed.), Handbook of Proof Theory, Amsterdam, North-Holland
(1998): 475-546.
- Lindström, P., “Provability Logic - A Short Introduction,”
Theoria, Vol. 52, No. 1-2 (1996): 19-61.
- Segerberg, K., An Essay in Classical Modal Logic, Uppsala,
Filosofiska Föreningen och Filosofiska Institutionen vid Uppsala Universitet
(1971).
- Svejdar, V., “On Provability Logic,” Nordic Journal of
Philosophy, Vol. 4 (2000): 95-116.
- Smorynski, C., Self-reference and Modal Logic, New York, Springer
Verlag (1995).
- Verbrugge, R. “Provability” in Borchert, D.M. (ed.), The Encyclopedia
of Philosophy: Supplement, New York, Simon and Schuster MacMillan (1996):
476-478.
- Visser, A., “Provability Logic,” in: W. Craig (ed.), Routledge
Encyclopedia of Philosophy, London, Routledge (1998): 793-797.
History
- Boolos, G. and Sambin, G., “Provability: The Emergence of a Mathematical
Modality,” Studia Logica, Vol. 50, No. 1 (1991): 1-23.
- Gödel, K., “Eine Interpretation des Intuitionistischen Aussagenkalküls,”
Ergebnisse eines Mathematischen Kolloquiums, Vol. 4 (1933): 39-40;
translation “An Interpretation of the Intuitionistic Propositional Calculus,”
in Gödel, K., Collected Works, ed. by Feferman, S. et al., Oxford and
New York: Oxford University Press (1995), Vol. 3: 296-302.
- Gödel, K., “Über Formal Unentscheidbare Sätze der Principia Mathematica
und Verwandter Systeme I,” Monatshefte für Mathematik und Physik,
Vol. 38 (1931): 173-198.
- Henkin, L., “A Problem Concerning Provability,” Journal of Symbolic
Logic, Vol. 17 (1952): 160.
- Hilbert, D. and Bernays, P. Grundlagen der Mathematik, volume 2.
Berlin, Heidelberg, New York, Springer-Verlag (1939).
- Lewis, C.I., “Implication and the Algebra of Logic,” Mind, Vol.
21 (1912): 522-531.
- Löb, M.H., “Solution of a Problem of Leon Henkin,” Journal of Symbolic
Logic, Vol. 20 (1955): 115-118.
- Smiley, T.J., “The Logical Basis of Ethics,” Acta Philosophica
Fennica, Vol. 16 (1963): 237-246.
Provability and Peano Arithmetic
- Davis, M., Computability and Unsolvability, New York, McGraw-Hill
(1958). Reprinted with an additional appendix, Dover 1983.
- Hájek, P. and Pudlák, P., Metamathematics of First-order
Arithmetic, Berlin, Springer-Verlag (1993).
- Solovay, R.M., “Provability Interpretations of Modal Logic,” Israel
Journal of Mathematics, Vol. 25 (1976): 287-304.
The scope of provability logic
- Artëmov, S.N. and Beklemishev, L.D., “On Propositional Quantifiers in
Provability Logic,” Notre Dame Journal of Formal Logic, Vol. 34 (1993):
401-419.
- Artëmov, S.N., “Nonarithmeticity of the Truth Predicate Logics of
Provability,” Doklady Akademii Nauk SSSR, Vol. 284 (1985): 270-271. In
Russian. English translation in: Soviet Mathematics Dokl., Vol. 32 (1985):
403-405.
- Artëmov, S.N., “Explicit Provability and Constructive Semantics,”
Bulletin of Symbolic Logic, Vol. 7 (2001): 1-36.
- Beklemishev, L.D., “On Bimodal Logics of Provability,” Annals of Pure
and Applied Logic, Vol. 68 (1994): 115-160.
- Beklemishev, L.D., “Bimodal Logics for Extensions of Arithmetical
Theories,” Journal of Symbolic Logic, Vol. 61 (1996): 91-124.
- Beklemishev, L.D., “Parameter-free Induction and Provably Total Computable
Functions,” Theoretical Computer Science, Vol. 224 (1999): 13-33.
- Beklemishev, L.D., Pentus, M. and Vereshchagin, N., “Provability,
Complexity, Grammars,” American Mathematical Society Translations,
Series 2, Vol. 192 (1999).
- Berarducci, A., “The Interpretability Logic of Peano Arithmetic,”
Journal of Symbolic Logic, Vol. 55 (1990): 1059-1089.
- Berarducci, A. and Verbrugge, R., “On the Provability Logic of Bounded
Arithmetic,” Annals of Pure and Applied Logic, Vol. 61 (1993): 75-93.
- Guaspari, D. and Solovay, R.M., “Rosser Sentences,” Annals of
Mathematical Logic, Vol. 16 (1979): 81-99.
- Iemhoff, R., “A Modal Analysis of some Principles of the Provability Logic
of Heyting Arithmetic,” in Zakharyashev, M. et al. (eds.), Advances in
Modal Logic, Vol. 2, Stanford, CSLI Publications (2000): 319-354.
- Iemhoff, R., “On the admissible rules of intuitionistic propositional
logic,” Jour. Symb. Logic, Vol. 66 (2001): 281-294.
- Jongh, D.H.J. de, Jumelet, M. and Montagna, F., “On the Proof of Solovay's
Theorem,” Studia Logica, Vol. 50 (1991): 51-70.
- McGee, V. and Boolos, G., “The Degree of the Set of Sentences of Predicate
Provability Logic that are True under Every Interpretation,” Journal of
Symbolic Logic, Vol. 52 (1987): 165-171.
- Montagna, F., “Polynomially and Superexponentially Shorter Proofs in
Fragments of Arithmetic,” Journal of Symbolic Logic, Vol. 57 (1992):
844-863.
- Shavrukov, V.Y., “The Logic of Relative Interpretability over Peano
Arithmetic,” Technical Report No. 5, Moscow, Steklov Mathematical Institute
(1988). In Russian.
- Shavrukov, V.Y., “A Note on the Diagonalizable Algebras of PA and ZF,”
Annals of Pure and Applied Logic, Vol. 61 (1993): 161-173.
- Shavrukov, V.Y., “Undecidability in Diagonalizable Algebras,” Journal
of Symbolic Logic, Vol. 62 (1997): 79-116.
- Svejdar, V., “Modal Analysis of Generalized Rosser Sentences,” Journal
of Symbolic Logic, Vol. 48 (1983): 986-999.
- Troelstra, A.S., Metamathematical Investigation of Intuitionistic
Arithmetic and Analysis, Berlin, Springer-Verlag (1973).
- Vardanyan, V.A., “Arithmetic Complexiy of Predicate Logics of Provability
and their Fragments,” Doklady Akademii Nauk SSSR, Vol. 288 (1986):
11-14. In Russian. English translation in Soviet Math. Dokl., Vol. 33
(1986): 569-572.
- Visser, A., Aspects of Diagonalization and Provability, Ph.D.
Thesis, Utrecht, University of Utrecht (1980).
- Visser, A., “Interpretability Logic,” in Petkov, P.P. (ed.),
Mathematical Logic, Proceedings of the Heyting 1988 Summer School in
Varna, Bulgaria, Boston, Plenum Press (1990): 175-209.
- Visser, A., “An Overview of Interpretability Logic,” in Kracht, M. et al.
(eds.), Advances in Modal Logic, Vol. 1, Stanford, CSLI Publications
(1998): 307-359.
- Visser, A., “Substitutions of
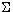 1 sentences: explorations
between intuitionistic propositional logic and intuitionistic arithmetic,”
Annals of Pure and Applied Logic, Vol. 114 (2002): 227-271.
1 sentences: explorations
between intuitionistic propositional logic and intuitionistic arithmetic,”
Annals of Pure and Applied Logic, Vol. 114 (2002): 227-271.
- Visser, A., “Rules and Arithmetics,” Notre Dame Journal of Formal
Logic, Vol. 40 (1) (1999): pp. 116-140.
Philosophical significance
- Davis, M., “Is Mathematical Insight Algorithmic,” Commentary on Roger
Penrose, The Emperor's New Mind, Behavioral and Brain Sciences, Vol.
13 (1990): 659-660.
- Davis, M., “How Subtle is Gödel's Theorem?,” Commentary on Roger Penrose,
The Emperor's New Mind, Behavioral and Brain Sciences, Vol. 16
(1993): 611-612.
- Quine, W.V., “Necessary Truth,” in Quine, W.V., The Ways of Paradox
and Other Essays, New York, Random House (1966): 48-56.
- Quine, W.V., “Three Grades of Modal Involvement,” in Proceedings of
the 11th International Congress of Philosophy, Amsterdam, North-Holland
(1953): 65-81. Also in in Quine, W.V., The Ways of Paradox and Other
Essays, New York, Random House (1966): 156-174.
artificial intelligence | Gödel, Kurt |
logic:
classical | logic:
intuitionistic | logic: modal | logic: relevance |
mathematics:
constructive | model theory |
possible worlds | Quine, Willard van Orman | Turing, Alan
A | B | C | D | E | F | G | H | I | J | K | L | M | N | O | P | Q | R | S | T | U | V | W | X | Y | Z
Stanford Encyclopedia of Philosophy
 A
A denote the Gödel number of
arithmetical formula A, the result of assigning a numerical code to
A. Let Prov be the formalized provability predicate for Peano
Arithmetic, which is of the form
denote the Gödel number of
arithmetical formula A, the result of assigning a numerical code to
A. Let Prov be the formalized provability predicate for Peano
Arithmetic, which is of the form 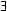 p Proof
(p,x). Here, Proof is the formalized proof predicate
of Peano Arithmetic, and Proof(p,x) stands for Gödel
number p codes a correct proof from the axioms of Peano Arithmetic of
the formula with Gödel number x. (For a more precise formulation, see
Smorynski (1985), Davis (1958)). Now, suppose that Peano Arithmetic proves
A
p Proof
(p,x). Here, Proof is the formalized proof predicate
of Peano Arithmetic, and Proof(p,x) stands for Gödel
number p codes a correct proof from the axioms of Peano Arithmetic of
the formula with Gödel number x. (For a more precise formulation, see
Smorynski (1985), Davis (1958)). Now, suppose that Peano Arithmetic proves
A 
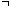 Prov
Prov A
A , then by Gödel's result,
A is not provable in Peano Arithmetic, and thus it is true, for in fact
the self-referential sentence A states “I am not provable”.
, then by Gödel's result,
A is not provable in Peano Arithmetic, and thus it is true, for in fact
the self-referential sentence A states “I am not provable”. B, can only be proved in Peano
Arithmetic in the trivial case that Peano Arithmetic already proves B
itself. This result, now called Löb's theorem, immediately answers Henkin's
question. (For a proof of Löb's theorem, see
B, can only be proved in Peano
Arithmetic in the trivial case that Peano Arithmetic already proves B
itself. This result, now called Löb's theorem, immediately answers Henkin's
question. (For a proof of Löb's theorem, see  A:
A:
 stands for provability in PA. Ironically,
the first time that the formalized version of Löb's theorem was stated as the
modal principle
stands for provability in PA. Ironically,
the first time that the formalized version of Löb's theorem was stated as the
modal principle
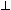 , a modal
operator
, a modal
operator  A is an abbreviation
for
A is an abbreviation
for 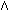
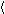 W,R,V
W,R,V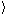 , where W is a set of
possible worlds, R is a binary accessibility relation on W,
and V is a valuation that assigns a truth value to each propositional
variable for each world in W. The pair F =
, where W is a set of
possible worlds, R is a binary accessibility relation on W,
and V is a valuation that assigns a truth value to each propositional
variable for each world in W. The pair F = 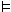 A, is defined inductively.
Let us repeat only the most interesting clause, the one for the provability
operator
A, is defined inductively.
Let us repeat only the most interesting clause, the one for the provability
operator 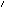 , if wRw
, if wRw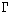 and all formulas A:
and all formulas A:
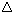 of
of 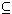
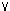
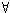 y
y 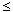 ss0
ss0 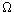 1, a theory which is somewhat
weaker than I
1, a theory which is somewhat
weaker than I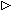 , where for a given arithmetical theory
T, the modal sentence A
, where for a given arithmetical theory
T, the modal sentence A 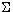 1 sentences: explorations
between intuitionistic propositional logic and intuitionistic arithmetic,”
Annals of Pure and Applied Logic, Vol. 114 (2002): 227-271.
1 sentences: explorations
between intuitionistic propositional logic and intuitionistic arithmetic,”
Annals of Pure and Applied Logic, Vol. 114 (2002): 227-271.