version history
|
A | B | C | D | E | F | G | H | I | J | K | L | M | N | O | P | Q | R | S | T | U | V | W | X | Y | Z
| This document uses XHTML/Unicode to
format the display. If you think special symbols are not displaying
correctly, see our guide Displaying
Special Characters. | |
last substantive content
change
|
Substructural Logics
Substructural logics are non-classical
logics weaker than classical logic, notable for the absence of
structural rules present in classical logic. These logics are motivated
by considerations from philosophy (relevant logics), linguistics (the Lambek
calculus) and computing (linear logic). In addition, techniques from
substructural logics are useful in the study of traditional logics such as
classical and intuitionistic logic. This article provides a brief overview of
the field of substructural logic. For a more detailed introduction, complete
with theorems, proofs and examples, the reader can consult the books and
articles in the Bibliography.
Logic is about logical consequence.
As a result, the conditional is a central notion in logic because of
its intimate connection with logical consequence. This connection is neatly
expressed in residuation condition:
p, q 
r if and only if
p
q → r
It says that r follows from
p together with q just when q → r
follows from p alone. The validity of the transition from q to
r (given p) is recorded by the conditional
q → r. (It is called residuation by analogy with
residuation in mathematics. Consider the connection between addition and
substraction. a + b = c if and only if a =
c − b. The resulting a (which is
c − b) is the residual, what is left of
c when b is taken away.)
However, there is one extra factor in the equation. Not only is there the
turnstile, for logical consequence, and the conditional, encoding consequence
inside the language of propositions, there is also the comma,
indicating the combination of premises. The behaviour of premise
combination is also important in determining the behaviour of the conditional.
As the comma's behaviour varies, so does the conditional. In this introduction
we will see how this comes about.
Weakening
It is one thing for p to be true. It is another for
the conditional q → p to be true. Yet, if ‘→’ is a material
conditional, q → p follows from p. It seems
worthwhile to understand how a conditional might work in the absence of
this inference. This is tied to the behaviour of premise combination, as can be
shown by this demonstration.
p
p
----------
p, q
p
-------------
p q →
p |
From the axiomatic p
p
(anything follows from itself) we deduce that p follows from
p together with q, and then by the residuation condition,
p
q → p. Given that we accept the residuation condition, and the
identity axiom at the start of the proof, we must reject the first step in the
proof if we are to deny that q → p follows from p.
This rule, which has the general form:
X
A
----------
X, Y
A |
is called the rule of
weakening. We step from a stronger statement, that A follows
from X to a possibly weaker one, that A follows from
X together with Y.
This rule may fail, given different notions of premise combination (the
notion encoded by the comma in X,Y). If the conditional → is
relevant (if to say that p → q is true is to say, at
least, that q truly depends on p) then the comma will
not satisfy weakening. We may indeed have A following from X,
without A following from X,Y, for it need not be the case that
A depends on X and Y together.
In relevant logics the rule of weakening fails on the other side
too, in that we wish this argument to be invalid too:
q
q
----------
p, q
q
-------------
p q →
q |
Again, q may follow
from q, but this doesn't mean that it follows from p
together with q, provided that "together with" is meant in an
appropriately strong sense. So, in relevant logics, the inference from an
arbitrary premise to a logical truth such as q → q may well
fail.
Commutativity
If the mode of premise combination is commutative (if
anything which follows from X, Y also follows from Y,
X) then we can reason as follows, using just the identity axiom and
residuation:
p → q p →
q
---------------------
p → q,
p
q
-------------------
p, p → q
q
---------------------
p (p → q) →
q |
In the absence of commutativity
of premise combination, this proof is not available. This is another simple
example of the connection between the behaviour of premise combination and that
of the conditional.
There are many kinds of conditional for which this inference fails. If → has
modal force (read it as entails) then we may have p
without also having (p → q) → q. It may be true that
Greg is a logician (p) and it is true that Greg's being a logician
entails Greg's being a philosopher (p → q) but this does not
entail that Greg is a philosopher. (There are many possibilities in
which the entailment (p → q) is true but q is not.)
So we have p true but (p → q) → q is not
true.
This makes sense when we consider premise combination. Here when we say
X,A B is
true, we are not just saying that B follows when we put X and
A together. If we are after a genuine entailment A →
B, then we want B to be true in any (related) possibility in which
A is true. So, X,A B says that in any
possibility in which A is true, so is B. These possibilities
mightn't satisfy all of X. (In classical theories of entailment, the
possibilities are those in which all that is taken as necessary in
X are true.)
If premise combination is not commutative, then residuation can go in
two ways. In addition to the residuation condition giving the behaviour
of →, we may wish to define a new arrow ← as follows:
p, q r if and only if
q
r ← p
For the left-to-right arrow we have
modus ponens in this direction:
p → q, p q
For the
right-to-left arrow, modus ponens is provable with the premises in the
opposite order:
p, q ← p q
This is a
characteristic of substructural logics. When we pay attention to what happens
when we don't have the full complement of structural rules, then new
possibilities open up. We uncover two conditionals underneath what was
previously one (in intuitionistic or classical logic).
Associativity
Here is another way that structural rules influence proof.
The associativity of premise combination provides the following proof:
p → q, p q
r → p, r p
---------------------------------
p → q,
(r → p, r) q
--------------------------
(p → q, r
→ p), r q
----------------------------
p → q, r
→ p r → q
-----------------------------------
p → q (r →
p) → (r →
q) |
This proof uses the
cut rule at the topmost step. The idea is that inferences can be
combined. If X A and Y(A) B (where
Y(A) is a structure of premises possibly including A one or
more times) then Y(X) B too (where Y(X)
is that structure of premises with those instances of A replaced by
X). In this proof, we replace the p in
p → q, p q by
r → p, r on the basis of the validity
of r → p, r p.
Contraction
A final important example is the rule of
contraction which dictates how premises may be reused. Contraction is
crucial in the inference of p → q from p →
(p → q)
p → (p → q) p → (p →
q)
p → q p →
q
----------------------------------
-----------------------
p → (p → q),
p
p → q
p → q, p
q
------------------------------------------------
(p
→ (p → q), p), p
q
--------------------------
p → (p →
q), p
q
-----------------------
p → (p →
q)
p → q |
These different
examples give you a taste of what can be done by structural rules. Not only do
structural rules influence the conditional, but they also have their effects on
other connectives, such as conjunction and disjunction (as we shall see below)
and negation (Dunn 1993; Restall 2000).
There are many different formal
systems in the family of substructural logics. These logics can be motivated in
different ways.
Relevant Logics
Many people have wanted to give an account of logical
validity which pays some attention to conditions of relevance. If
X,A
B holds, then X must somehow be relevant to
A. Premise combination is restricted in the following way. We may have
X
A without also having X,Y A . The new material
Y might not be relevant to the deduction. In the 1950s, Moh (1950),
Church (1951) and Ackermann (1956) all gave accounts of what a "relevant" logic
could be. The ideas have been developed by a stream of workers centred around
Anderson and Belnap, their students Dunn and Meyer, and many others. The
canonical references for the area are Anderson, Belnap and Dunn's two-volume
Entailment (1975 and 1992). Other introductions can be found in Read's
Relevant Logic and Dunn's "Relevance Logic and Entailment" (1986). A
more polemical introduction and defence of relevant logics can be found in
Routley, Plumwood, Meyer and Brady's Relevant Logics and Their Rivals.
Resource Consciousness
This is not the only way to restrict premise
combination. Girard (1987) introduced linear logic as a model for
processes and resource use. The idea in this account of deduction is that
resources must be used (so premise combination satisfies the relevance
criterion) and they do not extend indefinitely. Premises cannot be
re-used. So, I might have X,X A, which says that I can
use X twice to get A. I might not have X A, which says
that I can use X once alone to get A. A helpful introduction
to linear logic is given in Troelstra's Lectures on Linear Logic
(1992). There are other formal logics in which the contraction rule
(from X,X
A to X A) is absent. Most famous
among these are Łukasiewicz's many-valued logics. There has been a sustained
interest in logics without this rule because of Curry's paradox (Curry 1977,
Geach 1995; see also Restall 1994 in Other Internet Resources).
Order
Independently of either of these traditions, Joachim Lambek
considered mathematical models of language and syntax (Lambek 1958, 1961). The
idea here is that premise combination corresponds to composition of strings or
other linguistic units. Here X,X differs in content from X,
but in addition, X,Y differs from Y,X. Not only does the
number of premises used count but so does their order. Good
introductions to the Lambek calculus (also called categorial grammar)
can be found in books by Moortgat (1988) and Morrill (1994).
We have already seen a fragment of one way
to present substructural logics, in terms of proofs. We have used the
residuation condition, which can be understood as including two rules for the
conditional, one to introduce a conditional
X, A
B
----------------
X A →
B |
and another to
eliminate it.
X A → B
Y
A
--------------------------
X, Y
B |
Rules like these form the
cornerstone of a natural deduction system, and these systems are available for
the wide sweep of substructural logics. But proof theory can be done in other
ways. Gentzen systems operate not introducing and eliminating
connectives, but by introducing them both on the left and the right of the
turnstile of logical consequence. We keep the introduction rule above, and
replace the elimination rule by one introducing the conditional on the left:
X A
Y(B) C
--------------------------
Y(A → B,
X)
C |
This rule is more complex, but
it has the same effect as the arrow elimination rule: It says that if X
suffices for A, and if you use B (in some context Y)
to prove C then you could just as well have used A →
B together with X (in that same context Y) to prove
C, since A → B together with X gives you
B.
Gentzen systems, with their introduction rules on the left and the right,
have very special properties which are useful in studying logics. Since
connectives are always introduced in a proof (read from top to bottom)
proofs never lose structure. If a connective does not appear in the
conclusion of a proof, it will not appear in the proof at all, since connectives
cannot be eliminated.
In certain substructural logics, such as linear logic and the Lambek
calculus, and in the fragment of the relevant logic R without
disjunction, a Gentzen system can be used to show that the logic is
decidable, in that an algorithm can be found to determine whether or
not an argument X A is valid. This is done
by searching for proofs of X A in a Gentzen system.
Since premises of this conclusion must feature no language not in this
conclusion, and they have no greater complexity (in these systems), there are
only a finite number of possible premises. An algorithm can check if these
satisfy the rules of the system, and proceed to look for premises for these, or
to quit if we hit an axiom. In this way, decidability of some substructural
logics is assured.
However, not all substructural logics are decidable in this sense. Most
famously, the relevant logic R is not decidable. This is partly because
its proof theory is more complex than that of other substructural logics.
R differs from linear logic and the Lambek calculus in having a
straightforward treatment of conjunction and disjunction. In particular,
conjunction and disjunction satisfy the rule of distribution:
p & (q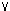 
r) (p & q)
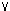(p &
r)
The natural proof of distribution in any proof system
uses both weakening and contraction, so it is not available in the relevant
logic R, which does not contain weakening. As a result, proof theories
for R either contain distribution as a primitive rule, or contain a
second form of premise combination (so called extensional combination,
as opposed to the intensional premise combination we have seen) which
satisfies weakening and contraction.
While the relevant logic R has a proof
system more complex than the substructural logics such as linear logic, which
lack distribution of (extensional) conjunction over disjunction, its
semantics is altogether more simple. A Routley-Meyer model for
the relevant logic R is comprised of a set of points P
with a three-place relation R on P. A conditional A →
B is evaluated at a world as follows:
A → B is true at x if and only if for
each y and z where Rxyz, if A is true at
y, B is true at z.
An argument is
valid in a model just when in any point at which the premises are true,
so is the conclusion. The argument A B → B is invalid
because we may have a point x at which A is true, but at which
B → B is not. We can have B → B fail to be
true at x simply by having Rxyz where B is true at
y but not at z.
The three place relation R follows closely the behaviour of the mode
of premise combination in the proof theory for a substructural logic. For
different logics, different conditions can be placed on R. For example,
if premise combination is commutative, we place a symmetry condition on
R like this: Rxyz if and only if Ryxz. Ternary
relational semantics gives us great facility to model the behaviour of
substructural logics. (The extent of the correspondence between the proof theory
and algebra of substructural logics and the semantics is charted in Dunn's work
on Gaggle Theory (1991) and is summarised in Restall's Introduction
to Substructural Logics (2000).) Furthermore, if conjunction and
disjunction satisfy the distribution axiom mentioned in the previous section,
they can be modelled straightforwardly too: a conjunction is true at a point
just when both conjuncts are true at that point, and a disjunction is true at a
point just when at least one disjunct is true there. For logics, such as linear
logic, without the distribution axiom, the semantics must be more
complex, with a different clause for disjunction required to invalidate the
inference of distribution.
It is one thing to use a semantics as a formal device to model a logic. It is
another to use a semantics as an interpretive device to apply
a logic. For logics like as the Lambek calculus, the interpretation of the
semantics is straightforward. We can take the points to be linguistic units, and
the ternary relation to be the relation of composition (Rxyz if and
only if x concatenated with y results in z). For the
relevant logic R and its interpretation of natural language conditionals,
more work must be done in identifying what features of reality the formal
semantics models. Some of this work is reported in the article on relevant logic in
this Encyclopedia.
A comprehensive bibliography on relevant
logic was put together by Robert Wolff and can be found in Anderson, Belnap and
Dunn 1992. The bibliography in Restall 2000 (see Other Internet
Resources) is not as comprehensive as Wolff's, but it does include material
up to the last part of the 1990s.
Books on Substructural Logic and Introductions to the Field
- Anderson, A.R., and Belnap, N.D., 1975, Entailment: The Logic of
Relevance and Necessity, Princeton, Princeton University Press, Volume I.
- Anderson, A.R., Belnap, N.D. Jr., and Dunn, J.M., 1992,
Entailment, Volume II, Princeton, Princeton University Press
[This book and the previous one summarise the work in relevant logic in
the Anderson--Belnap tradition. Some chapters in these books have other
authors, such as Robert K. Meyer and Alasdair Urquhart.]
- Dunn, J.M., 1986, "Relevance Logic and Entailment" in F. Guenthner and D.
Gabbay (eds.), Handbook of Philosophical Logic, Volume 3, Dordrecht:
Reidel pp 117--224.
[A summary of work in relevant logic in the
Anderson--Belnap tradition. An updated version of this essay, co-authored with
Restall, will appear in the new edition of the Handbook of Philosophical
Logic.]
- Moortgat, Michiel, 1988, Categorial Investigations: Logical Aspects of
the Lambek Calculus Foris, Dordrecht.
[Another introduction to the
Lambek calculus.]
- Morrill, Glyn, 1994, Type Logical Grammar: Categorial Logic of
Signs Kluwer, Dordrecht
[An introduction to the Lambek calculus.]
- Read, S., 1988, Relevant Logic, Oxford: Blackwell.
[An
introduction to relevant logic from a distinct philosophical perspective.]
- Restall, Greg, 2000, An Introduction to Substructural Logics,
Routledge. (online
précis)
[A comprehensive introduction to the field of substructural
logics.]
- Routley, R., Meyer, R.K., Plumwood, V., and Brady, R., 1983, Relevant
Logics and its Rivals, Volume I, Atascardero, CA: Ridgeview.
[Another
distinctive account of relevant logic, this time from an Australian
philosophical perspective.]
- Schroeder-Heister, Peter, and Dosen, Kosta, (eds), 1993, Substructural
Logics, Oxford University Press.
[An edited collection of essays on
different topics in substructural logics, from different traditions in the
field.]
- Troestra, Anne, 1992, Lectures on Linear Logic, CSLI
Publications
[A quick, easy-to-read introduction to Girard's linear logic.]
Other Works Cited
- Ackermann, Wilhelm, 1956, "Begründung Einer Strengen Implikation",
Journal of Symbolic Logic 21 113-128.
- Church, Alonzo, 1951, "The Weak Theory of Implication", in
Kontroliertes Denken: Untersuchungen zum Logikkalkül und zur Logik der
Einzelwissenschaften, Kommissions-Verlag Karl Alber, edited by A. Menne,
A. Wilhelmy and H. Angsil, 22-37.
- Curry, Haskell B., 1977, Foundations of Mathematical Logic, Dover
(originally published in 1963).
- Dunn, J.M., 1991, "Gaggle Theory: An Abstraction of Galois Connections and
Residuation with Applications to Negation and Various Logical Operations", in
Logics in AI, Proceedings European Workshop JELIA 1990, Lecture notes
in Computer Science, volume 476 Springer-Verlag.
- Dunn, J.M., 1993, "Star and Perp," Philosophical Perspectives
7 331-357.
- Geach, P. T., 1955, "On Insolubilia," Analysis 15 71-72.
- Girard, Jean-Yves, 1987, "Linear Logic," Theoretical Computer
Science 50 1-101.
- Lambek, Joachim, 1958, "The Mathematics of Sentence Structure",
American Mathematical Monthly 65 154-170.
- Lambek, Joachim, 1961, "On the Calculus of Syntactic Types", in
Structure of Language and its Mathematical Aspects, edited by R.
Jakobson, (Proceedings of Symposia in Applied Mathematics, XII).
- Moh Shaw-Kwei, 1950, "The Deduction Theorems and Two New Logical Systems,"
Methodos 2 56-75.
- Slaney, John, 1994, "Finite Models for some Substructural Logics,"
Automated Reasoning Project Technical Report TR-ARP-04-94. Available as either
a DVI
or Postscript
file.
logic: modal | logic:
paraconsistent | logic: relevance
A | B | C | D | E | F | G | H | I | J | K | L | M | N | O | P | Q | R | S | T | U | V | W | X | Y | Z
Stanford Encyclopedia of Philosophy