version history
|
A | B | C | D | E | F | G | H | I | J | K | L | M | N | O | P | Q | R | S | T | U | V | W | X | Y | Z
| This document uses XHTML/Unicode to
format the display. If you think special symbols are not displaying
correctly, see our guide Displaying
Special Characters. | |
last substantive content
change
|
Supertasks
Supertasks have posed problems for philosophy since the time
of Zeno of Elea. The term ‘supertask’ is new but it designates an idea already
present in the formulation of the old motion paradoxes of Zeno, namely the idea
of an infinite number of actions performed in a finite amount of time. The main
problem lies in deciding what follows from the performance of a supertask. Some
philosophers have claimed that what follows is a contradiction and that
supertasks are, therefore, logically impossible. Others have denied this
conclusion, and hold that the study of supertasks can help us improve our
understanding of the physical world, or even our theories about it.
A supertask may be defined as an
infinite sequence of actions or operations carried out in a finite interval of
time. The terms ‘action’ and ‘operation’ must not be understood in their usual
sense, which involves a human agent. Human agency may be involved but it is not
necessary. To show this, let us see how actions can be characterised precisely
without any references to man. We will assume that at each instant of time the
state of the world relevant to a specific action can be described by a set S of
sentences. Now an action or operation applied to a state of the world results in
a change in that state, that is, in the set S corresponding to it. Consequently,
an arbitrary action a will be defined (Allis and Koetsier [1995]) as a change in
the state of the world by which the latter changes from state S before the
change to state a(S) after it. This means that an action has a beginning and an
end, but does not entail that there is a finite lapse of time between them. For
instance, take the case of a lamp that is on at t = 0 and remains so until t =
1, an instant at which it suddenly goes off. Before t =1 the state of the lamp
(which is the only relevant portion of the world here) can be described by the
sentence ‘lamp on’, and after t =1 by the sentence ‘lamp off’, without there
being a finite lapse of time between the beginning and the end of the action.
Some authors have objected to this consequence of the definition of action, and
they might be right if we were dealing with the general philosophical problem of
change. But we need not be concerned with those objections at this stage, since
in the greatest majority of the relevant supertasks instantaneous actions (i.e.
actions without any duration) can be replaced by actions lasting a finite amount
of time without affecting the analysis at any fundamental point.
There is a particular type of supertask called hypertasks. A
hypertask is a non-numerable infinite sequence of actions or operations carried
out in a finite interval of time. Therefore, a supertask which is not a
hypertask will be a numerable infinite sequence of actions or operations carried
out in a finite interval of time. Finally, a task can be defined as a finite
sequence of actions or operations carried out in a finite interval of time.
To gain a
better insight into the fundamental nature of the philosophical problem posed by
supertasks, consider the distinction between tasks in general (finite sequences
of actions of the type (a1, a2, a3, … ,
an)) and one particular type of supertasks, namely those consisting
of an infinite sequence of actions of the type (a1, a2,
a3, … , an, … ) and thus having the same type of order as
the natural order of positive integers: 1, 2, 3, … , n, … (it is customary to
denote this type of order with letter ‘w’ and so the related supertasks
can be called supertasks of type w).
In the case of a task T = (a1, a2, a3, … ,
an) it is natural to say that T is applicable in state S if:
a1 is applicable to S,
a2 is applicable
to a1(S),
a3 is applicable to
a2(a1(S)),
… , and,
an is applicable
to an-1(an-2(… (a2(a1(S)))…
)).
The successive states of the world relevant to task T can be
defined by means of the finite sequence of sets of sentences:
S, a1(S), a2(a1(S)),
a3(a2(a1(S))), …,
an(an-1(an-2 (…
(a2(a1(S)))…))),
whose last term will
therefore describe the relevant state of the world after the performance of T.
Or, equivalently, the state resulting from applying T to S will be T(S) =
an(an-1(an-2 (…
(a2(a1(S)))… ))).
Now take the case of a
supertask T = (a1, a2, a3, …, an,
…). Let us give the name Tn to the task which consists in performing
the first n actions of T. That is, Tn = (a1,
a2, a3, …, an). Now it is natural to say that T
is applicable in state S if Tn is applicable in S for each natural
number n, and, obviously,
Tn(S) = an(an-1(an-2
(…(a2(a1(S)))…))).
The successive states of
the world relevant to supertask T can be described by means of the infinite
sequence of sets of sentences:
S, T1(S), T2(S), …, Tn(S),
…
A difficulty arises, however, when we want to specify the set of
sentences which describe the relevant state of the world after the performance
of supertask T, because the infinite sequence above lacks a final term. Put
equivalently, it is difficult to specify the relevant state of the world
resulting from the application of supertask T to S because there seems to be no
final state resulting from such an application. This inherent difficulty is
increased by the fact that, by definition, supertask T is performed in a finite
time, and so there must exist one first instant of time t* at which it can be
said that the performance happened. Now notice that the world must naturally be
in a certain specific state at t*, which is the state resulting from the
application of T, but that, nevertheless, we have serious trouble to specify
this state, as we have just seen.
Since we have defined
supertasks in terms of actions and actions in terms of changes in the state of
the world, there is a basic indeterminacy regarding what type of processes
taking place in time should be considered supertasks, which is linked to the
basic indeterminacy that there is regarding which type of sets of sentences are
to be allowed in descriptions of the state of the world and which are not. For
this reason, there are some processes that would be regarded as supertasks by
virtually every philosopher and some about which opinions differ. For an
instance of the first sort of process, take the one known as ‘Thomson's lamp’.
Thomson's lamp is basically a device consisting of a lamp and a switch set on an
electrical circuit. The switch can be in one of just two positions and the lamp
has got to be lit — when the switch is in position ‘on’ — or else dim — when the
switch is in position ‘off’. Assume that initially (at t = 12 A.M., say) the
lamp is dim and that it is thenceforth subject to the following infinite
sequence of actions: when half of the time remaining until t* = 1 P.M. has gone
by, we carry out the action a1 of turning the switch into position
‘on’ and, as a result, the lamp is lit (a1 is thus performed at t =
1/2 P.M.); when half the time between the performance of a1 and t* =
1 P.M. has gone by, we carry out action a2 of turning to the switch
into position ‘off’ and, as a result, the lamp is dim (a2 is thus
performed at t = 1/2 + 1/4 P.M.); when half the time between the performance of
a2 and t* = 1 P.M. has gone by, we carry out the action of turning
the switch into position ‘on’ and, as a result, the lamp is lit (a3
is thus performed at t = 1/2 + 1/4 + 1/8), and so on. When we get to instant t*
= 1 P.M. we will have carried out an infinite sequence of actions, that is, a
supertask T = (a1, a2, a3, … , an, …
). If, for the sake of simplicity, we are only concerned about the evolution of
the lamp (not the switch) the state of the world relevant to the description of
our supertask admits of only two descriptions, one through the unitary set of
sentences {lamp lit} and the other through the set {lamp dim}.
As an instance of the second sort of processes we referred to above, those
about which no consensus has been reached as to whether they are supertasks, we
can take the process which is described in one of the forms of Zeno's dichotomy
paradox. Suppose that initially (at t = 12 A.M., say) Achilles is at point A
(x = 0) and moving in a straight line, with a constant velocity
v = 1 km/h, towards point B (x = 1), which is 1 km. away from
A. Assume, in addition, that Achilles does not modify his velocity at any point.
In that case, we can view Achilles's run as the performance of a supertask, in
the following way: when half the time until t* = 1 P.M. has gone by, Achilles
will have carried out the action a1 of going from point x =
0 to point x = 1/2 (a1 is thus performed in the interval of
time between t =12 A.M. and t = 1/2 P.M.), when half the time from the end of
the performance of a1 until t* = 1 P.M. will have elapsed, Achilles
will have carried out the action a2 of going from point x =
1/2 to point x = 1/2 + 1/4 (a2 is thus performed in the
interval of time between t = 1/2 P.M. and t = 1/2 + 1/4 P.M.), when half the
time from the end of the performance of a2 until t* = 1 P.M. will
have elapsed, Achilles will have carried out the action a3 of going
from point x = 1/2 + 1/4 to point x = 1/2 + 1/4 + 1/8
(a3 is thus performed in the interval of time between t = 1/2 + 1/4
P.M. and t = 1/2 + 1/4 + 1/8 P.M.), and so on. When we get to instant t* = 1
P.M., Achilles will have carried out an infinite sequence of actions, that is, a
supertask T = (a1, a2, a3, … , an, …
), provided we allow the state of the world relevant for the description of T to
be specified, at any arbitrary instant, by a single sentence: the one which
specifies Achilles's position at that instant. Several philosophers have
objected to this conclusion, arguing that, in contrast to Thomson's lamp,
Achilles's run does not involve an infinity of actions (acts) but of
pseudo-acts. In their view, the analysis presented above for Achilles's run is
nothing but the breakdown of one process into a numerable infinity of
subprocesses, which does not make it into a supertask. In Allis and Koetsier's
words, such philosophers believe that a set of position sentences is not always
to be admitted as a description of the state of the world relevant to a certain
action. In their opinion, a relevant description of a state of the world should
normally include a different type of sentences (as is the case with Thomson's
lamp) or, in any case, more than simply position sentences.
In section
1.2 I have pointed out and illustrated the fundamental philosophical problem
posed by supertasks. Obviously, one will only consider it a problem if one deems
the concepts employed in its formulation acceptable. In fact, some philosophers
reject them, because they regard the very notion of supertask as problematic, as
leading to contradictions or at least to insurmountable conceptual difficulties.
Among these philosophers the first well-known one is Zeno of Elea.
Consider the dichotomy
paradox in the formulation of it given in section 1.3. According to Zeno,
Achilles would never get to point B (x = 1) because he would first have
to reach the mid point of his run (x = 1/2), after that he would have
to get to the mid point of the span which he has left (x = 1/2 + 1/4),
and then to the mid point of the span which is left (x = 1/2 + 1/4 +
1/8), and so on. Whatever the mid point Achilles may reach in his journey, there
will always exist another one (the mid point of the stretch that is left for him
to cover) that he has not reached yet. In other words, Achilles will never be
able to reach point B and finish his run. According to Owen (Owen [1957-58]), in
this as well as in his other paradoxes, Zeno was concerned to show that the
Universe is a simple, global entity which is not comprised of different parts.
He tried to demonstrate that if we take to making divisions and subdivisions we
will obtain absurd results (as in the dichotomy case) and that we must not yield
to the temptation of breaking up the world. Now the notion of supertask entails
precisely that, division into parts, as it involves breaking up a time interval
into successive intervals. Therefore, supertasks are not feasible in the
Zenonian world and, since they lead to absurd results, the notion of supertask
itself is conceptually objectionable.
In stark contrast to Zeno, the dichotomy paradox is standardly solved by
saying that the successive distances covered by Achilles as he progressively
reaches the mid points of the spans he has left to go through — 1/2, 1/4, 1/8,
1/16, … — form an infinite series 1/2 + 1/4 + 1/8 + 1/16 + … whose sum is 1.
Consequently, Achilles will indeed reach point B (x = 1) at t* = 1 P.M.
(which is to be expected if he travels with velocity v = 1 km/h, as has
been assumed). Then there is no problem whatsoever in splitting up his run into
smaller sub-runs and, so, no inherent problem about the notion of supertask. An
objection can be made, however, to this standard solution to the paradox: it
tells us where Achilles is at each instant but it does not explain where Zeno's
argument breaks down. Importantly, there is another objection to the standard
solution, which hinges on the fact that, when it is claimed that the infinite
series 1/2 + 1/4 + 1/8 + 1/16 + … adds up to 1, this is substantiated by the
assertion that the sequence of partial sums 1/2, 1/2 + 1/4, 1/2 + 1/4 + 1/8, …
has limit 1, that is, that the difference between the successive terms of the
sequence and number 1 becomes progressively smaller than any positive integer,
no matter how small. But it might be countered that this is just a patch up: the
infinite series 1/2 + 1/4 + 1/8 + … seems to involve infinite sums and thus the
performance of a supertask, and the proponent of the standard solution is in
fact presupposing that supertasks are feasible just in order to justifiy that
they are. To this the latter might reply that the assertion that the sum of the
series is 1 presupposes no infinite sum, since, by definition, the sum of a
series is the limit to which its partial (and so finite) sums approach. His
opponent can now express his disagreement with the response that the one who
supports the standard solution is deducing a matter of fact (that Achilles is at
x = 1 at t* = 1 P.M.) from a definition pertaining to the arithmetic of
infinite series, and that it is blatantly unacceptable to deduce empirical
propositions from mere definitions.
Before
concluding our discussion of the arguments connected with Zeno's dichotomy
paradox which have been put forward against the conceptual feasibility of
supertasks, we should deal with the so-called inverse dichotomy of Zeno, which
can also be formulated as a supertask, but whose status as a logical possibility
seems to some philosophers to be even more doubtful than that of the direct
version expounded in section 2.1. The process involved in the paradox of inverse
dichotomy admits of a supertask kind of description, as follows. Suppose that at
t = 12 A.M. Achilles is at point A (x = 0) and wishes to do the action
of reaching point B (x = 1). In order to do this action he must first
of all go from point A to the mid point b1 (x = 1/2) of the
span AB that he wishes to cover. In order to do this, he must in turn first do
the action of going from point A to the mid point b2 (x =
1/4) of the span Ab1 that he wishes to cover, and so on . In order to
reach B, Achilles will have to accomplish an infinite sequence of actions, that
is, a supertask T* = (… , an, … , a3, a2,
a1), provided we allow the state of the world relevant to the
description of T* to be specified, at a given arbitrary instant, by a single
sentence, the one specifying Achilles's position at that instant. Notice in the
first place that T* has the same type of order as the natural order of negative
integers: … , -n, … , -3, -2, -1 (such order type is usually denoted with the
expression ‘w*’ and the related supertasks can therefore be called
supertasks of type w*). The philosophical problem connected with
supertasks of type w, already discussed in section 1.2 above, does not
arise now because the set of sentences which describes the relevant state of the
world after the performance of supertask T* is obviously a1(S), with
S the set of sentences describing the initial relevant state of the world. But
as the successive states of the world after S in relation to T* can be described
by means of the infinite sequence of sets of sentences … , an(S), … ,
a3(S), a2(S), a1(S), some philosophers think it
puzzling and unacceptable that the initial set of sentences in that sequence
cannot be specified. This really means that we cannot specify which is the
action in supertask T* that should be carried out first and that we consequently
ignore how to begin. Isn't that proof enough that supertasks of type w*
are impossible? Chihara (1965), for example, says that Zeno's inverse dichotomy
is even more problematic than the direct one, since Achilles is supposed to be
capable of doing something akin to counting the natural numbers in reverse
order. In his opinion, it is just as impossible for Achilles to start his run —
if viewed as a supertask of type w* — as it is to start this reverse
counting process.
Thomson
(1954-55) was convinced that he could show supertasks to be logically
impossible. To this end, he made up the lamp example analysed in section 1.3,
since known as ‘Thomson's lamp’. Thomson argued that the analysis of the
workings of his lamp leads to contradiction, and therefore the supertask
involved is logically impossible. But then, to the extent that this supertask is
representative of ‘genuine’ supertasks, all genuine supertasks are impossible.
Thomson's argument is simple. Let us ask ourselves what the state of the lamp is
at t* = 1 P.M. At that instant the lamp cannot be lit, the reason being the way
we manipulate it: we never light the lamp without dimming it some time later.
Nor can the lamp be dim, because even if it is dim initially, we light it and
subsequently never dim it without lighting it back again some time later.
Therefore,at t* = 1 P.M. the lamp can be neither dim nor lit. However, one of
its functioning conditions is that it must be either dim or lit. Thus, a
contradiction arises. Conclusion: Thomson's lamp or, better, the supertask
consisting in its functioning is logically impossible. Now is Thomson's argument
correct? Benacerraf (1962) detected a serious flaw in it. Let us in principle
distinguish between the series of instants of time in which the actions
ai of the supertask are performed (which will be called the t-series)
and the instant t* = 1 P.M., the first instant after the supertask has been
accomplished. Thomson's argument hinges on the way we act on the lamp, but we
only act on it at instants in the t-series, and so what can be deduced logically
from this way of acting will apply only to instants in the t-series. As t* = 1
P.M. does not belong to the t-series, it follows that Thomson's supposed
conclusion that the lamp cannot be lit at t* is fallacious, and so is his
conclusion that it cannot be dim at t*. The conditions obtaining in the lamp
problem only enable us to conclude that the lamp will be either dim or else lit
but not both at t* = 1 P.M., and this follows from the fact that this exclusive
disjunction was presupposed from the start to be true at each and every instant
of time, independently of the way in which we could act on the lamp in the
t-series of instants of time. What cannot be safely inferred is which one of
these two states -dim or lit- the lamp will be in at t* = 1 P.M. or,
alternatively, the state of the lamp at t* = 1 P.M. is not logically determined
by what has happened before that instant. This consequence tallies with what was
observed in section 2.1 about the fallacy committed by adherents to the standard
solution against Zeno: they seek to deduce that at instant t* = 1 P.M. Achilles
will be at point B from an analysis of the sub-runs performed by him before that
instant, that is, they assume that Achilles's state at t* follows logically from
his states at instants previous to t*, and in so assuming they make the same
mistake as Thomson.
Thomson (1954-55) put forward one more argument against the logical
possibility of his lamp. Let us assign to the lamp the value 0 when it is dim
and the value 1 when it is lit. Then lighting the lamp means adding one unity
(going from 0 to 1) and dimming it means subtracting one unity (going from 1 to
0). It thus seems that the final state of the lamp at t* = 1 P.M., after an
infinite, and alternating, sequence of lightings (additions of one unity) and
dimmings (subtractions of one unity), should be described by the infinite series
1-1+1-1+1… If we accept the conventional mathematical definition of the sum of a
series, this series has no sum, because the partial sums 1, 1-1, 1-1+1, 1-1+1-1,
… , etc. take on the values 1 and 0 alternatively, without ever approaching a
definite limit that could be taken to be the proper sum of the series. But in
that case it seems that the final state of the lamp can neither be dim (0) nor
lit (1), which contradicts our assumption that the lamp is at all times either
dim or lit. Benacerraf's (1962) reply was that even though the first, second,
third, … , n-th partial sum of the series 1-1+1-1+1… does yield the state of the
lamp after one, two, three, … , n actions ai (of lighting or
dimming), it does not follow from this that the final state of the lamp after
the infinite sequence of actions ai must of necessity be given by the
sum of the series, that is, by the limit to which its partial sums progressively
approach. The reason is that a property shared by the partial sums of a series
does not have to be shared by the limit to which those partial sums tend. For
instance, the partial sums of the series 0.3 + 0.03 + 0.003 + 0.0003 + … are
0.3, 0.3 + 0.03 = 0.33, 0.3 + 0.03 + 0.003 = 0.333,… , all of them, clearly,
numbers less than 1/3; however, the limit to which those partial sums tend (that
is, the sum of the original series) is 0.3333… , which is precisely the number
1/3.
Another one of the
classical arguments against the logical possibility of supertasks comes from
Black (1950-51) and is constructed around the functioning of an infinity machine
of his own invention. An infinity machine is a machine that can carry out an
infinite number of actions in a finite time. Black's aim is to show that an
infinity machine is a logical impossibility. Consider the case of one such
machine whose sole task is to carry a ball from point A (x = 0) to
point B (x = 1) and viceversa. Assume, in addition, that initially (at
t = 12 A.M., say) the ball is at A and that the machine carries out the
following infinite sequence of operations: when half the time until t* = 1 P.M.
has gone by, it does the action a1 of taking the ball from position A
to position B (a1 is thus carried out at t = 1/2 P.M.); when half the
time between the performance of a1 and t* = 1 P.M. has gone by, it
does the action a2 of taking the ball from position B to position A
(a2 is thus carried out at t = 1/2 + 1/4 P.M.); when half the time
between the performance of a2 and t* = 1 P.M. has gone by, the
machine does the action a3 of taking the ball from position A to
position B (a3 is thus performed in t = 1/2 + 1/4 + 1/8 P.M.), and so
on. When we get to instant t* = 1 P.M. the machine will have carried out an
infinite sequence of actions, that is, a supertask T = (a1,
a2, a3, … , an, … ). The parallelism with
Thomson's lamp is clear when it is realised that the ball in position A
corresponds to the dim lamp and the ball in position B corresponds to the lit
lamp. Nevertheless, Black believes that by assuming that at each instant the
ball is either in A or else in B (and note that assuming this means that the
machine transports the ball from A to B and viceversa instantaneously, but we
need not be worried by this, since all that we are concerned with now is logical
or conceptual possibility, not physical possibility), he can deduce, by a
totally different route from Thomson's based on the symmetrical functioning of
his machine, a contradiction regarding its state at t* = 1 P.M.. However,
Benacerraf's criticisms also applies to Black's argument. In effect, the latter
hinges on how the machine works, and as this has only been specified for
instants of time previous to t* = 1 P.M., it follows that what can be logically
inferred from the functioning of the machine is only applicable to those
instants previous to t* = 1 P.M.. Black seeks to deduce a contradiction at t* =
1 P.M. but he fails at the same point as Thomson: whatever happens to the ball
at t* = 1 P.M. cannot be a logical consequence of what has happened to it
before. Of course, one can always specify the functioning of the machine for
instants t greater than or equal to 1 P.M. by saying that at all those instants
the machine will not perform any actions at all, but that is not going to help
Black. His argument is fallacious because he seeks to reach a logical conclusion
regarding instant t* = 1 P.M. from information relative to times previous to
that instant.. In the standard argument against Zeno's dichotomy one could
similarly specify Achilles's position at t* = 1 P.M. saying, for instance, that
he is at B (x = 1), but there is no way that this is going to get us a
valid argument out of a fallacious one, which seeks to deduce logically where
Achilles will be at t* = 1 P.M. from information previous to that instant of
time.
The cases dealt with above are examples of how Benacerraf's
strategy can be used against supposed demonstrations of the logical
impossibility of supertasks. We have seen that the strategy is based on the idea
that
(I) the state of a system at an instant t* is not a logical
consequence of which states he has been in before t* (where by ‘state’ I mean
‘relevant state of the world’, see section 1.1)
and occasionally on
the idea that
(II) the properties shared by the partial sums of a series do not
have to be shared by the limit to which those partial sums
tend.
Since the partial sums of a series make up a succession (of
partial sums), (II) may be rewritten as follows:
(III) the properties shared by the terms of a succession do not
have to be shared by the limit to which that succession tends.
If we
keep (I), (II) and (III) well in mind, it is easy not to yield to the perplexing
implications of certain supertasks dealt with in the literature. And if we do
not yield to the perplexing results, we will also not fall into the trap of
considering supertasks conceptually impossible. (III), for instance, may be used
to show that it is not impossible for Achilles to perform the supertasks of the
inverse and the direct dichotomy of Zeno. Take the case of the direct dichotomy:
the limit of the corresponding succession of instants of time t1,
t2, t3, … at which each one of Achilles's successive
sub-runs is finished can be the instant at which Achilles's supertask has been
accomplished, even if such a supertask is not achieved at any one of the
instants in the infinite succession t1, t2, t3,
… (all of this in perfect agreement with (III)).
As a corollary it may be said that
supertasks do not seem to be intrinsically impossible. The contradictions that
they supposedly give rise to may be avoided if one rejects certain unwarranted
assumptions that are usually made. The main such assumption, responsible for the
apparent conceptual impossibility of supertasks, is that properties which are
preserved after a finite number of actions or operations will likewise be
preserved after an infinite number of them. But that is not true in general. For
example, we saw in section 1.2 above that the relevant state of the world after
the performance of a task T = (a1, a2, … , an)
on the relevant state S was logically determined by T and by S (and was
an(an-1(an-2(…
(a2(a1(S)))…)))), but we have now learned that after the
performance of a supertask T = (a1, a2, a3, …,
an, …) it is not (that is the core of Benacerraf's critique). The
same sort of uncritical assumptions seem to be in the origin of infinity
paradoxes in general, in which certain properties are extrapolated from the
finite to the infinite that are only valid for the finite, as when it is assumed
that there must be more numbers greater than zero than numbers greater than 1000
because all numbers greater than 1000 are also greater than zero but not
viceversa (Galileo's paradox). In conclusion, if some supertasks are
paradoxical, it is not because of any inherent inconsistency of the notion of
supertask. This opinion is adhered to by authors such as Earman and Norton
(1996).
We have gone
through several arguments for the conceptual impossibility of supertasks and
counterarguments to these. Those who hold that supertasks are conceptually
possible may however not agree as to whether they are also physically possible.
In general, when this issue is discussed in the literature, by physical
possibility is meant possibility in relation with certain broad physical
principles, laws or ‘circumstances’ which seems to operate in the real world, at
least as far as we know. But it is a well-known fact that authors do not always
agree about which those principles, laws or circumstances are.
In our model of Thomson's
lamp we are assuming that at each moment the switch can be in just one of two
set positions (‘off’, ‘on’). If there is a fixed distance d between them, then
clearly, since the switch swings an infinite number of times from the one to the
other from t = 12 A.M. until t* = 1 P.M., it will have covered an infinite
distance in one hour. For this to happen it is thus necessary for the speed with
which the switch moves to increase unboundedly during this time span. Grünbaum
has taken this requirement to be physically impossible to fulfil. Grünbaum
(1970) believes that there is a sort of physical impossibility of a purely
kinematical nature (kinematical impossibility) and describes it in more precise
terms by saying that a supertask is kinematically impossible if:
a) At least one of the moving bodies travels at an unboundedly
increasing speed,
b) For some instant of time t*, the position of at least one of the moving
bodies does not approach any defined limit as we get arbitrarily closer in
time to t*.
It is clear then that the Thomson's lamp supertask,
in the version presented so far, is kinematically (and eo ipso physically)
impossible, since not only does the moving switch have to travel at a speed that
increases unboundedly but also -because it oscillates between two set positions
which are a constant distance d apart- its position does not approach any
definite limit as we get closer to instant t* = 1 P.M., at which the supertask
is accomplished. Nevertheless, Grünbaum has also shown models of Thomson's lamp
which are kinematically possible. Take a look at Figure 1, in which the switch
(in position ‘on’ there) is simply a segment AB of the circuit connecting
generator G with lamp L. The circuit segment AB can shift any distance upwards
so as to open the circuit in order for L to be dimmed. Imagine we push the
switch successively upwards and downwards in the way illustrated in Figure 2, so
that it always has the same velocity v = 1.
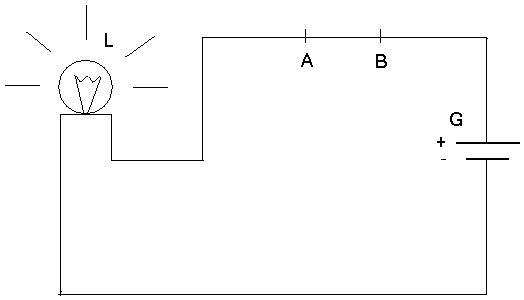
Figure 1
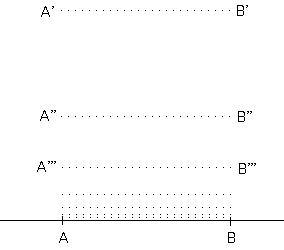
Figure 2
The procedure is the following.
Initially (t = 0) the switch is in position A′B′ (lamp dim) a height of 0.2
above the circuit and moving downwards (at v = 1). At t = 0.2 it will
be in position AB (lamp lit) and will begin moving upwards (v = 1). At
t = 0.2 + 0.01 it will be in position A″B″ (lamp dim) and will begin moving
downwards (v = 1). At t = 0.2 + 0.01 + 0.01 = 0.2 + 0.02 it will be in
position AB (lamp lit) and will begin moving upwards (v = 1). At t =
0.2 + 0.02 + 0.001 it will be in position A′′′B′′′ (lamp dim), and so on.
Obviously, between t = 0 and t* = 0.2 + 0.02 + 0.002 + … = 0.2222… = 2/9, the
lamp is in the states ‘dim’ and ‘lit’ an infinite number of times, and so a
supertask is accomplished. But this supertask is not kinematically impossible,
because it has been so designed that the switch always moves with velocity
v = 1 — and, therefore, condition (a) for kinematical impossibility is
not fulfilled — and that, additionally, as we get closer to the limit time t* =
2/9 (the only one which could cause us any trouble) the switch approaches more
and more a well-defined limit position, position AB (lamp lit) -and, therefore,
condition b) for kinematical impossibility is not fulfilled either. Once the
kinematical possibility has been established, what is the state of the lamp at
t* = 2/9? What has been said so far does not enable us to give a determinate
answer to this question (just as the obvious kinematical possibility of
Achilles's supertask in the dichotomy paradox does not suffice to determine
where Achilles will be at t* = 1 P.M.), but there exists a ‘natural’ result. It
seems intuitively acceptable that the position the switch will occupy at t* =
2/9 will be position AB, and so the lamp will be lit at that instant. There is
no mysterious asymmetry about this result. Figure 3 shows a model of Thomson's
lamp with a switch that works according to exactly the same principles as
before, but which will yield the ‘natural’ result that the lamp will in the end
be dim at t* = 2/9. In effect, the switch will now finally end up in the
‘natural’ position AB at t* = 2/9 and will thereby bring about an electrical
short-circuit that will make all the current in the generator pass through the
cable on which the switch is set, leaving nothing for the more resistant path
where the lamp is.
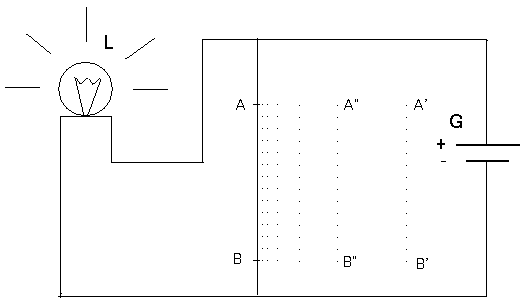
Figure 3
There are some who believe that the
very fact that there exist Thomson's lamps yielding an intuitive result of ‘lamp
lit’ when the supertask is accomplished but also other lamps whose intuitive
result is ‘lamp dim’ brings up back to the contradiction which Thomson thought
to have found originally. But we have nothing of that sort. What we do have is
different physical models with different end-results. This does not contradict
but rather corroborates the results obtained by Benacerraf: the final state is
not logically determined by the previous sequence of states and operations. This
logical indeterminacy can indeed become physical determinacy, at least
sometimes, depending on what model of Thomson's lamp is employed.
A conspicuous instance of a supertask which is kinematically impossible is
the one performed by Black's infinity machine, whose task it is to transport a
ball from position A (x = 0) to position B (x = 1) and from B
to A an infinite number of times in one hour. As with the switch in our first
model of Thomson's lamp, it is obvious that the speed of the ball increases
unboundedly (and so condition a) for impossibility is met), while at the same
time, as we approach t* = 1 P.M., its position does not tend to any defined
limit, due to the fact that it must oscillate continuously between two set
positions A and B one unity distance apart from each other (and so also
condition b) for impossibility is met).
Up to this point we have seen
examples of supertasks which are conceptually possible and, among these, we have
discovered some which are also physically possible. For the latter to happen we
had to make sure that at least some requirements were complied with which,
plausibly, characterise the processes that can actually take place in our world.
But some definitive statement remains to be made about the philosophical problem
posed by supertasks: what the state of the world is after they have been
accomplished. The principles of physical nature which have so far been appealed
to do not enable us to pronounce on this matter. The question thus arises
whether some new principle of a physical nature can be discovered which holds in
the real world and is instrumental in answering the question what the state of
the world will be after a supertask. That discovery would allow us to resolve a
radical indeterminacy which still persists -the reader will remember that even
in the case of Achilles's dichotomy supertask we were quite unable to prove that
it would conclude with Achilles in point B (x = 1). In Section 2.1 we
saw that such proof cannot be obtained by recourse to the mathematical theory of
infinite series exclusively; why should it be assumed that this abstract theory
is literally applicable to the physical universe? After all, amounts of money
are added up applying ordinary arithmetic but, as Black reminded us, velocities
cannot be added up according to ordinary arithmetic.
Since Benacerraf's critique, we know that there is no logical connection
between the position of Achilles at t* = 1 P.M. and his positions at instants
previous to t* = 1 P.M. Sainsbury [1988] has tried to bridge the gap opened by
Benacerraf. He claims that this can be achieved by drawing a distinction between
abstract space of a mathematical kind and physical space. No distinction between
mathematical and physical space has to be made, however, to attain that goal;
one need only appeal to a single principle of physical nature, which is,
moreover, simple and general, namely, that the trajectories of material bodies
are continuous lines. To put it more graphically, what this means is that we can
draw those trajectories without lifting our pen off the paper. More precisely,
that the trajectory of a material body is a continuous line means that, whatever
the instant t, the limit to which the position occupied by the body tends as
time approaches t coincides precisely with the position of the body at t.
Moreover, the principle of continuity is highly plausible as a physical
hypothesis: the trajectories of all physical bodies in the real world are in
fact continuous. What matters is that we realise that, aided by this principle,
we can now finally demonstrate that after the accomplishment of the dichotomy
supertask, that is, at t* = 1 P.M., Achilles will be in point B (x =
1). We know, in fact, that as the time Achilles has spent running gets closer
and closer to t* = 1 P.M., his position will approach point x = 1 more
and more, or, equivalently, we know that the limit to which the position
occupied by Achilles tends as time get progressively closer to t* = 1 P.M. is
point B (x = 1). As Achilles's trajectory must be continuous, by the
definition of continuity (applied to instant t = t* = 1 P.M.) we obtain that the
limit to which the position occupied by Achilles tends as time approaches t* = 1
P.M. coincides with Achilles's position at t* = 1 P.M. Since we also know that
this limit is point B (x = 1), it finally follows that Achilles's
position at t* = 1 P.M. is point B (x = 1). Now is when we can spot the
flaw in the standard argument against Zeno mentioned in section 2.1, which was
grounded on the observation that the sequence of distances covered by Achilles
(1/2, 1/2 + 1/4, 1/2 + 1/4 + 1/8, … ) has 1 as its limit. This alone does not
suffice to conclude that Achilles will reach point x = 1, unless it is
assumed that if the distances run by Achilles have 1 as their limit, then
Achilles will as a matter of fact reach x = 1, but assuming this
entails using the principle of continuity. This principle affords us a rigorous
demonstration of what, in any event, was already plausible and intuitively
‘natural’: that after having performed the infinite sequence of actions
(a1, a2, a3, … , an, … ) Achilles
will have reached point B (x = 1). In addition, now it is easy to show
how, with a switch like the one in Figure 2, Thomson's lamp in Figure 1 will
reach t* = 2/9 with its switch in position AB and will therefore be lit. We have
in fact already pointed out (3.1) that in this case, as we get closer to the
limit time t* = 2/9, the switch indefinitely approaches a well-defined limit
position -position AB. Due to the fact that the principle of continuity applies
to the switch, because it is a physical body, this well-defined limit position
must coincide precisely with the position of the switch at t* = 2/9. Therefore,
at t* = 2/9 the latter will be in positon AB and, consequently, the lamp will be
lit. By the same token, it can also be shown that the lamp in Figure 3 will be
dim at time t* = 2/9.
In Section 3.2, the
principle of continuity helped us find the final state resulting from the
accomplishment of a supertask in cases in which there exists a ‘natural’ limit
for the state of the physical system involved as time progressively approaches
the instant at which the supertask is achieved. Now it is considerably more
problematic to apply this principle to supertasks for which there is no
‘natural’ limit. For an example, let us consider Black's infinity machine,
introduced in Section 2.4, and let us ask ourselves where the ball will be at
instant t* = 1 P.M. at which the supertask is achieved. We can set up a reductio
ad absurdum type of argument, as follows. Assume that at t* = 1 P.M. the ball
were to occupy position P, that it was in point P. According to the principle of
continuity, it follows that the limit to which the position occupied by the ball
tends as time approaches t* = 1 P.M. is precisely position P. We know, though,
that Black's infinity machine makes the ball oscillate more and more quickly
between the fixed points A (x = 0) and B (x = 1) as we get
closer to t* = 1 P.M., so the position of the ball does not approach any
definite limit as we get closer to t* = 1 P.M. This conclusion patently
contradicts what follows from the principle of continuity. Therefore, the
assumption that, after Black's supertask is achieved (t* = 1 P.M.), the ball is
at point P leads to contradiction with the principle of continuity. Thus, the
ball cannot be at point P at t* = 1 P.M., and as the point can be any, given
that it has been chosen arbitrarily, the ball cannot be at any single one of the
points, which means that at t* = 1 P.M. the ball has ceased to exist. This funny
conclusion is consistent with the principle of continuity, as we have just seen,
but it enters into contradiction with what could be termed the ‘postulate of
permanence’: no material body (and by that we mean a given quantity of matter)
can go out of existence all of a sudden, without leaving any traces. The
postulate of permanence seems to characterise our world at least as evidently as
the principle of continuity. Notice in particular that certain physical bodies
(particles) may dematerialise, but that is not inconsistent with the postulate
of permanence since such a dematerialisation leaves an energy trace (which is
not true of Black's ball). Consequently, we can see that the case Black's
infinity machine is one in which the principles of continuity and permanence
turn out to be mutually inconsistent. As long as we do not give up any of them,
we are forced to accept that such an infinity machine is physically impossible.
As we do not know exactly
what laws of nature there are, it goes without saying that the question whether
a particular supertask is physically possible (that is, compatible with those
laws) cannot be given a definitive answer in general. What we have done in 3
above is rather to set out necessary conditions for physical possibility which
are plausible (such as the principle of continuity) and sufficient conditions
for physical impossibility which are likewise plausible (such as Grünbaum's
criterion of kinematical impossibility). In this section we shall look into a
problem related to the one just dealt with, but one to which a definitive answer
can be given: the problem of deciding whether a certain supertask is possible
within the framework of a given physical theory, that is, whether it is
compatible with the principles of that theory. These are two distinct problems.
At this stage our object are theories whereas in 3 above we were concerned with
the real world. What we are after is supertasks formulated within the defined
framework of a given physical theory which can tell us something exciting and/or
new about that theory. We will discover that this search will lead us right into
the heart of basic theoretical problems.
Classical dynamics is a theory that studies the motion
of physical bodies which interact among themselves in various ways. The vast
majority of interesting examples of supertasks within this theory have been
elaborated under the assumption that the particles involved only interact with
one another by means of elastic collisions, that is, collisions in which no
energy is dissipated. We shall see here that supertasks of type w* give
rise to a new form of indeterministic behaviour of dynamical systems. The most
simple type of case (Pérez Laraudogoitia [1996]) is illustrated by the particle
system represented in Figure 4 at three distinct moments. It consists of an
infinite set of identical point particles P1, P2,
P3, … , Pn, … arranged in a straight line. Take the
situation depicted in Figure 4A first. In it P1 is at one unity
distance from the coordinate origin O, P2 at a distance 1/2 of O,
P3 at a distance 1/3 of O and so on. In addition, let it be that all
the particles are at rest, except for P1, which is approaching O with
velocity v = 1. Suppose that all this takes place at t = 0. Now we will
employ
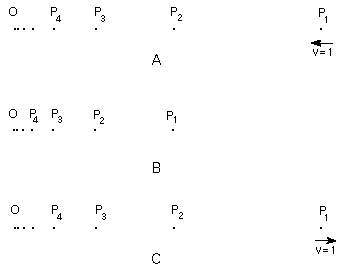
Figure 4
the well-known dynamic theorem by
which if two identical particles undergo an elastic collision then they will
exchange their velocities after colliding. If our particles P1,
P2, P3, … collide elastically, it is easy to predict what
will happen after t = 0 with the help of this theorem. In the event that
P1 were on its own, it would reach O at t = 1, but in fact it will
collide with P2 and lie at rest there, while P2 will
acquire velocity v = 1. If P1 and P2 were on
their own, then it would be P2 that would reach O at t = 1, but
P2 will in fact collide with P3, and lie at rest there,
while P3 will acquire velocity v = 1. Again, it can be said
that if P1, P2 and P3 were on their own, then
it is P3 that would reach O at t = 1, but in actual fact it will
collide with P4 and lie at rest there, while P4 will
acquire velocity v = 1, and so on. From the foregoing it follows that
no particle will get to O at t = 1, because it will be impeded by a collision
with another particle. Therefore, at t = 1 all the particles will already lie at
rest, which yields the configuration in Figure 4B. Since P1 stopped
when it collided with P2, it will occupy the position P2
had initially (at t = 0). Similarly, P2 stopped after colliding with
P3 and so it will occupy the position P3 had initially (at
t = 0), … , etc. If we view each collision as an action (which is plausible,
since it involves a sudden change of velocities), it turns out that between t =
0 and t = 1 our evolving particle system has performed a supertask of type
w. The second dynamic theorem we will make use of says that if a
dynamic process is possible, then the process resulting from inverting the
direction in which all the bodies involved in it move is also possible. Applying
this to our case, if the process leading from the system in the situation
depicted in Figure 4A to the situation depicted in Figure 4B is possible (and we
have just seen it is), then the process obtained by simply inverting the
direction in which the particles involved move will also be possible. This new
possible process does not bring the system from configuration 4B back to
configuration 4A but rather changes it into configuration 4C (as the direction
in which P1 moves must be inverted). As the direct process lasts one
time unity (from t = 0 to t = 1), so will the inverse process, and as in the
direct process the system performs a supertask of type w, in the
inverse process it will perform one of type w*. What is interesting
about this new supertask of type w*? What's interesting is that it
takes the system from a situation (4B) in which all its component particles are
at rest to another situation (4C) in which not all of them are. This means that
the system has self-excited, because no external influence has been exerted on
it, and, what is more, it has done so spontaneously and unpredictably, because
the supertask can set off at any instant and there is no way of predicting when
it will happen. We have found a supertask of type w* to be the source
of a new form of dynamical indeterminism. The reason we speak of indeterminism
is because there is no initial movement to the performance of the supertask. The
system self-excites in such a way that each particle is set off by a collision
with another one, and it is the ordinal type w* of the sequence of
collisions accomplished in a finite time that guarantees movement, without the
need for a ‘prime mover’. Now movement without a ‘prime mover’ is precisely what
characterises the dynamical indeterminism linked to supertasks of type
w*.
The previous model of supertask in the form of spontaneous self-excitation is
valid in relativistic classical dynamics as well as non-relativistic classical
dynamics and can also be extended - though not in a completely obvious way, see
Pérez Laraudogoitia [2001] - to the Newtonian theory of universal gravitation.
The core idea behind indeterministic behaviour in all these cases is that the
configuration of a physical system consisting of a denumerable infinite number
of parts can be such that the solutions to the dynamic equations - in principle,
one for each one of the parts - turn out to be coupled. A particular case of
this situation (but probably the most important case, as it is the one that can
be generalised more straightforwardly) is that in which the connection between
solutions stems from the fact that the dynamic equations themselves are coupled
as a result of the configuration of the system. Norton [1999] has availed
himself of precisely this possibility, thus introducing a model of spontaneous
self-excitation in quantum mechanics. Even though the indeterminism vanishes in
this case when the normalizability of the state vector is imposed, this does not
make his proposal any less interesting: after all, the free particle solutions
to Schrodinger's equation are not normalizable either.
The physics of supertasks in the context of the other major closed physical
theory, general relativity, will be the topic of the following two subsections.
Within relativity theory, supertasks have been approached from a radically
different perspective from the one adopted here so far. This new perspective is
inherently interesting, since it links the problem of supertasks up with the
relativistic analysis of the structure of space-time. To get an insight into the
nature of that connection, let us first notice that, according to the theory of
relativity, the duration of a process will not be the same in different
reference systems but will rather vary according to the reference system within
which it is measured. This leaves open the possibility that a process which
lasts an infinite amount of time when measured within reference system O may
last a finite time when measured within a different reference system O’.
The supertask literature has needed to exploit space-times with sufficiently
complicated structure that global reference systems cannot be defined in them.
In these and other cases, the time of a process can be represented by its
‘proper time’. If we represent a process by its world-line in space-time, the
proper time of the process is the time read by a good clock that moves with the
process along its world-line. A familiar example of its use is the problem of
the twins in special relativity. One twin stays home on earth and grows old.
Forty years of proper time, for example, elapses along his world-line. The
travelling twin accelerates off into space and returns to find his sibling forty
years older. But much less time — say only a year of proper time — will have
elapsed along the travelling twin world-line if he has accelerated to
sufficiently great speeds.
If we take this into account it is easily seen that the definition of
supertask that we have been using is ambiguous. In section 1 above we defined a
supertask as an infinite sequence of actions or operations carried out in a
finite interval of time. But we have not specified in whose proper time we
measure the finite interval of time. Do we take the proper time of the process
under consideration? Or do we take the proper time of some observer who watches
the process? It turns out that relativity theory allows the former to be
infinite while the latter is finite. This fact opens new possibilities for
supertasks. Relativity theory thus forces us to disambiguate our definition of
supertask, and there is actually one natural way to do it. We can use Black's
idea — presented in 2.4 — of an infinity machine, a device capable of performing
a supertask, to redefine a supertask as an infinite sequence of actions or
operations carried out by an infinity machine in a finite interval of the
machine's own proper time measured within the reference system associated to the
machine. This redefinition of the notion of supertask does not change anything
that has been said until now; our whole discussion remains unaffected so long as
‘finite interval of time’ is read as ‘finite interval of the machine's proper
time’. This notion of supertask, disambiguated so as to accord with relativity
theory, will be denoted by the expression ‘supertask-1’. Thus:
Supertask-1: an infinite sequence of actions or operations carried
out by an infinity machine in a finite interval of the machine's proper
time.
However we might also imagine a machine that carries out an
infinite sequence of actions or operations in an infinite machine proper time,
but that the entire process can be seen by an observer in a finite amount of the
observer's proper time.
It is convenient at this stage to introduce a contrasting notion:
Supertask-2: an infinite sequence of actions or operations carried
out by a machine in a finite interval of an observer's proper
time.
While we did not take relativity theory into account, the
notions of supertask-1 and supertask-2 coincided. The duration of an interval of
time between two given events is the same for all observers. However in
relativistic spacetimes this is no longer so and the two notions of supertasks
become distinct. Even though all supertasks-1 are also supertasks-2, there may
in principle be supertasks-2 which are not supertasks-1. For instance, it could
just so happen that there is a machine (not necessarily an infinity machine)
which carries out an infinite number of actions in an interval of its own proper
time of infinite duration, but in an interval of some observer's proper time of
finite duration. Such a machine would have performed a supertask-2 but not a
supertask-1.
The distinction between supertasks-1 and supertasks-2 is certainly no
relativistic hair-splitting. Why? Because those who hold that, while
conceptually possible, supertasks are physically impossible (this seems to be
the position adopted by Benacerraf and Putnam [1964], for instance) usually mean
that supertasks-1 are physically impossible. But from this, it does not follow
that supertasks-2 must also be physically impossible. Relativity theory thus
adds a brand-new, exciting extra dimension to the challenge presented by
supertasks. Earman and Norton (1996), who have studied this issue carefully, use
the name ‘bifurcated supertasks’ to refer specifically to supertasks-2 which are
not supertasks-1, and I will adopt this term.
What shape does the philosophical problem posed by
supertasks — introduced in Section 1.2 — take on now? Remember that the problem
lay in specifying the set of sentences which describe the state of the world
after the supertask has been performed. The problem will now be to specify the
set of sentences which describe the relevant state of the world after the
bifurcated supertask has been performed. Before this can done, of course, the
question needs to be answered whether a bifurcated supertask is physically
possible. Given that we agree that compatibility with relativity theory is a
necessary and sufficient condition of physical possibility, we can reply in the
affirmative.
Pitowsky (1990) first showed how this compatibility might arise. He
considered a Minkowski spacetime, the spacetime of special relativity. He showed
that an observer O* who can maintain a sufficient increase in his acceleration
will find that only a finite amount of proper time elapses along his world-line
in the course of the complete history of the universe, while other unaccelerated
observers would find an infinite proper time elapsing on theirs.
Let us suppose that some machine M accomplishes a bifurcated supertask in
such a way that the infinite sequence of actions involved happens in a finite
interval of an observer O's proper time. If we imagine such an observer at some
event on his world-line, all those events from which he can retrieve information
are in the ‘past light cone’ of the observer. That is, the observer can receive
signals travelling at or less than the speed of light from any event in his past
light cone. The philosophical problem posed by the bifurcated supertask
accomplished by M has a particularly simple solution when the infinite sequence
of actions carried out by M is fully contained within the past light cone of an
event on observer O's world-line. In such a case the relevant state of the world
after the bifurcated supertask has been performed is M's state, and this, in
principle, can be specified, since O has causal access to it. Unfortunately, a
situation of this type does not arise in the simple bifurcated supertask devised
by Pitowsky (1990). In his supertask, while the accelerated observer O* will
have a finite upper bound on the proper time elapsed on his world-line, there
will be no event on his world-line from which he can look back and see an
infinity of time elapsed along the world-line of some unaccelerated
observer.
To find a spacetime in which the philosophical problem posed by bifurcated
supertasks admits of the simple solution that has just been mentioned, we will
move from the flat spacetime of special relativity to the curved spacetimes of
general relativity. One type of spacetime in the latter class that admits of
this simple solution has been dubbed Malament-Hogarth spacetime, from the names
of the first scholars to use them (Hogarth [1992]). An example of such a
spacetime is an electrically charged black hole (the Reissner-Nordstroem
spacetime). A well known property of black holes is that, in the view of those
who remain outside, unfortunates who fall in appear to freeze in time as they
approach the event horizon of the black hole. Indeed those who remain outside
could spend an infinite lifetime with the unfortunate who fell in frozen near
the event horizon. If we just redescribe this process from the point of view of
the observer who does fall in to the black hole, we discover that we have a
bifurcated supertask. The observer falling in perceives no slowing down of time
in his own processes. He sees himself reaching the event horizon quite quickly.
But if he looks back at those who remain behind, he sees their processes sped up
indefinitely. By the time he reaches the event horizon, those who remain outside
will have completed infinite proper time on their world-lines. Of course, the
cost is high. The observer who flings himself into a black hole will be torn
apart by tidal forces and whatever remains after this would be unable to return
to the world in which he started.
The possibility of
supertasks has interesting consequences for the philosophy of mathematics. To
start with, take a well-known unsolved mathematical problem, for example that of
knowing whether Goldbach's conjecture is or is not correct. Goldbach's
conjecture asserts that any even number greater than 2 is the sum of two prime
numbers. Nobody has been capable of showing whether this is true yet, but if
supertasks are possible, that question can be resolved. Let us, to that effect,
perform the supertask of type w consisting in the following sequence of
actions: action a1 involves checking whether the first pair greater
than 2 (number 4) is the sum of two prime numbers or not; let this action be
accomplished at t = 0.3 P.M.; action a2 involves checking whether the
second pair greater than 2 (number 6) is the sum of two prime numbers or not;
let this action be accomplished at t = 0.33 P.M.; action a3 involves
checking whether the third pair greater than 2 (number 8) is the sum of two
prime numbers or not; let this action be accomplished at t = 0.333 P.M., and so
on. It is clear that at t = 0.33333… = 1/3 P.M., the instant at which the
supertask has already been performed, we will have checked all the pairs greater
than 2, and, therefore, will have found some which is not the sum of two prime
numbers or else will have found all of them to be the sum of two prime numbers.
In the first case, we will know at t = 1/3 P.M. that Goldbach's conjecture is
false; in the seocnd case we will know at t = 1/3 P.M. that it is true. Weyl
(1949) seems to have been the first to point to this intriguing method -the use
of supertaks- for settling mathematical questions about natural numbers. He,
however, rejected it on the basis of his finitist conception of mathematics;
since the performance of a supertask involves the successive carrying out of an
actual infinity of actions or operations, and the infinity is impossible to
accomplish, in his view. For Weyl, taking the infinite as an actual entity makes
no sense. Nevertheless, there are more problems here than Weyl imagines, at
least for those who ground their finitist philosophy of mathematics on
intuitionism à la Brouwer. That is because Brouwer's rejection of actual
infinity stems from the fact that we, as beings, are immersed in time. But this
in itself does not mean that all infinities are impossible to accomplish, since
an infinity machine is also ‘a being immerse in time’ and that in itself does
not prevent the carrying out of the infinity of successive actions a supertask
is comprised of. It goes without saying that one can adhere to a constructivist
philosophy of mathematics (and the consequent rejection of actual infinity) for
diferent reasons from Brouwer's; supertasks will still not be the right kind of
objet to study either.
As Benacerraf and Putnam (1964) have observed, the acknowledgement that
supertasks are possible has a profound influence on the philosophy of
mathematics: the notion of truth (in arithmetic, say) would no longer be
doubtful, in the sense of dependent on the particular axiomatisation used. The
example mentioned earlier in connection with Goldbach's conjecture can indeed be
reproduced and generalised to all other mathematical statements involving
numbers (although, depending on the complexity of the statement, we might need
to use several infinity machines instead of just one), and so, consequently,
supertasks will enable us to decide on the truth or falsity of any arithmetical
statement; our conclusion will no longer depend on provability in some formal
system or constructibility in a more or less strict intuitionistic sense. This
conclusion seems to lead to a Platonist philosophy of mathematics.
However, the situation here is more subtle than the previous comments
suggest.Above I introduced a supertask of type w that can settle the
truth or falsity of Goldbach's conjecture, but the reference (essential in it)
to time contrasts with the lack of specification regarding how to make the
necessary computations.When one tries to make up for this omission one discovers
that the defence of Platonism is more debatable than it seems at first sight.
Davies [2001] has proposed a model of an infinite machine (an infinite machine
is a computer which can carry out an infinite number of computations within a
finite length of time) based on the Newtonian dynamics of continuous media which
reveals the nature of the difficulty. One cannot attempt to decide on
mathematical questions such as Goldbach's conjecture by using a mechanical
computer which carries out operations at an increasing speed, as if it were a
Turing machine. The reason is that the different configurations the computer
adopts at increasingly short intervals of time eventually (if the conjecture is
true) lead to a paradox of the type of Thomson's lamp, where (if we do not
assume continuity in the sense of section 3.2) the final state of the computer
is indeterminate, which makes it useless for our purpose. Davies's clever
solution consists in assuming an infinite machine capable of building a replica
of itself that has twice its own memory but is smaller and works at greater
speed. The replica can in its turn build another (even smaller and quicker)
replica of itself and so on. With the details Davies gives about the working of
his infinite machines, it is clear that they will in no case lead to an
indeterminacy paradox (since each replica carries out only a finite part of the
task).The problem is that to settle questions like Goldbach's conjecture (if, as
I said above, it is true) a numerable (actual) infinity of replicating machines
is required, and this will surely be rejected by anyone who, like intuitionists,
has a strong dislike of the actual infinity. In more abstract words, the
mathematical theory that models the computation process presupposes a Platonic
conception of the infinite and thus begs the question by, circularly, supporting
Platonism.
Similar comments can be made about the implications of
supertasks for the philosophy of mathematics if one only accepts the possibility
of bifurcated supertasks. Of course, a bifurcated supertask performed in a
non-Malament-Hogarth space-time would not be so interesting in this sense. The
obvious reason is that we would not even have a sound procedure to determine the
truth or falsity of Goldbach's conjecture seen in 5.1 by means of the
performance of an infinite sequence of actions of order type w. To really have a
safe decision procedure in this simple case (as in other, more complex ones)
there must necessarily exist an instant of time at which it can be said that the
supertask has been accomplished. Otherwise, in the event that the machine finds
a counterexample to Goldbach's conjecture we will know it to be false, but in
the event of the machine finding none we will not be able to tell that it is
true, because for this there must exist an instant of time by which the
supertask has been accomplished and at which we can say something like: "the
supertask has been performed and the machine has found no counterexamples to
Goldbach's conjecture; therefore, the conjecture is true". It follows that, in
the case of a bifurcated supertask, possessing a sound decision procedure on
Goldbach's conjecture requires the existence of an observer O such that the
infinite sequence of actions (of order type w) carried out by the machine lies
within the past light cone of an event on observer O's world-line. But this is
equivalent to saying that the relativistic space-time in which the bifurcated
supertask is performed is a Malament-Hogarth space-time, and this realisation is
one of the main reasons why this sort of relativistic space-times have been
studied in the literature.
At first sight, the intuitionistic criticism of the possibility of supertasks
is less effective in the case of bifurcated supertasks, because in this latter
case it is not required that there is any sort of device capable of carrying out
an infinite number of actions or operations in a finite time (measured in the
reference system associated to the device in question, which is the natural
reference system to consider). In contrast, from the possibility of bifurcated
supertasks in Malament-Hogarth space-times strong arguments seem to follow
against an intuitionistic philosophy of mathematics. But, again, one must be
very cautious at this point, as we were at the end of our previous section 5.1.
The mathematical theory which models a bifurcated supertask is general
relativity, and this theory, as it fully embraces classical mathematical
analysis, entails a strong commitment to the - intuitionistically unacceptable -
objective status of the set of all natural numbers. It is difficult to believe,
therefore, that a radical constructivist lets himself be influenced by the
current literature on bifurcated supertasks. This does not make that literature
less interesting, as, in establishing unthought-of connections between
computability and the structure of space-time, it enriches (as does the existing
literature on supertasks in general) the set of consequences that can be derived
from our most interesting physical theories.
- Allis, V. and Koetsier, T., 1991, ‘On Some Paradoxes of the Infinite’,
British Journal for the Philosophy of Science, 42,
pp. 187-194
- Allis, V. and Koetsier, T., 1995, ‘On Some Paradoxes of the Infinite II’,
British Journal for the Philosophy of Science, 46,
pp. 235-247
- Alper, J.S. and Bridger, M., 1998, ‘Newtonian Supertasks: A Critical
Analysis’ Synthese, 114, pp. 355-369
- Alper, J.S., Bridger, M., Earman , J. and Norton , J.D., 2000, ‘What is a
Newtonian System? The Failure of Energy Conservation and Determinism in
Supertasks’ Synthese, 124, pp.281-293
- Aristotle, Physics, (W. Charlton, trans.), Oxford: Oxford
University Press, 1970
- Benacerraf, P., 1962, ‘Tasks, Super-Tasks, and Modern Eleatics’,
Journal of Philosophy, LIX, pp. 765-784; reprinted
in Salmon [1970]
- Benacerraf, P. and Putnam, H., 1964, Introduction, Philosophy of
Mathematics: Selected Readings, P. Benacerraf and H. Putnam (eds.), 2nd
edition, Cambridge: Cambridge University Press, pp. 1-27
- Benardete, J.A., 1964, Infinity: An Essay in Metaphysics, Oxford:
Clarendon Press
- Berresford, G. C., 1981, ‘A Note on Thomson's Lamp "Paradox"’,
Analysis, 41, pp. 1-7
- Black, M., 1950-1, ‘Achilles and the Tortoise’, Analysis,
XI, pp. 91-101; reprinted in Salmon [1970]
- Black, M., 1954, Problems of Analysis, Ithaca: Cornell University
Press
- Black, R., 2002, "Solution to a small infinite puzzle", Analysis,
62.4, pp. 345-346
- Bokulich, A., 2003, "Quantum measurement and supertasks",
International Studies in the Philosophy of Science,
17.2, pp. 127-136
- Bostock, D., 1972-73, ‘Aristotle, Zeno and the Potential Infinite’,
Proceedings of the Aristotelian Society, 73, pp.
37-51
- Burke, M.B., 1984, ‘The Infinitistic Thesis’, The Southern Journal of
Philosophy, 22, pp. 295-305
- Burke, M.B., 2000, ‘The Impossibility of Superfeats’, The Southern
Journal of Philosophy, XXXVIII, pp.207-220
- Burke, M.B., 2000, ‘The Staccato Run: a Contemporary Issue in the Zenonian
Tradition’ ,The Modern Schoolman, LXXVIII, pp.1-8
- Bridger, M., and Alper, J. S., 1999, ‘On the Dynamics of
Perez-Laraudogoitia's Supertask’, Synthese, 119, pp.
325-337
- Chihara, C., 1965, ‘On the Possibility of Completing an Infinite Task’,
Philosophical Review, LXXIV, pp. 74-87
- Clark, P., and Read, S., 1984, ‘Hypertasks’, Synthese,
61, pp. 387-390
- Cooke, M.C., 2003, "Infinite Sequences: Finitist Consequence", British
Journal for the Philosophy of Science, 54, pp. 591-599
- Cotogno, P., 2003, "Hypercomputation and the Physical Church-Turing
Thesis", British Journal for the Philosophy of Science,
54 , pp. 181-223
- Davies, E.B., 2001, "Building Infinite Machines", British Journal for
the Philosophy of Science, 52 , pp. 671-682
- Earman, J., 1994, Bangs, Crunches, Shrieks, and Whimpers:
Singularities and Acausalities in Relativistic Spacetimes, New York:
Oxford University Press
- Earman, J., and Norton, J.D., 1993, ‘Forever Is a Day: Supertasks in
Pitowsky and Malament-Hogarth Spacetimes’, Philosophy of Science,
60, pp. 22-42
- Earman, J., and Norton, J. D., 1996, ‘Infinite Pains: The Trouble with
Supertasks’, in Benacerraf and His Critics, A. Morton and S. Stich
(eds.), Oxford: Blackwell, pp. 231-261.
- Earman, J., and Norton, J. D., 1998, ‘Comments on Laraudogoitia's
"Classical Particle Dynamics, Indeterminism and a Supertask"’, British
Journal for the Philosophy of Science, 49, pp. 123-133
- Faris, J. A., 1996, The Paradoxes of Zeno, Aldershot: Avebury
- Forrest, P., 1999, "Supertasks and material objects", Logique et
Analyse, 166-167, pp. 441-446
- Friedman, K.S., 2002, "A small infinite puzzle", Analysis,
62.4, pp. 344-345
- Gale, R. M. (ed.), 1968, The Philosophy of Time, London:
MacMillan
- Glazebrook, T., 2001, ‘Zeno Against Mathematical Physics’, Journal of
the History of Ideas, 62, pp.193-210
- Groarke, L., 1982, ‘Zeno's Dichotomy: Undermining the Modern Response’,
Auslegung, 9, pp. 67-75
- Grünbaum, A. 1950-52 ‘Messrs. Black and Taylor on Temporal Paradoxes’,
Analysis, 11-12, pp. 144-148
- Grünbaum, A., 1967, Modern Science and Zeno's Paradoxes,
Middletown, CT: Wesleyan University Press
- Grünbaum, A., 1968, ‘Are "Infinity Machines" Paradoxical?’,
Science, CLIX, pp. 396-406
- Grünbaum, A., 1969, ‘Can an Infinitude of Operations be Performed in a
Finite Time?’, British Journal for the Philosophy of Science,
20, pp. 203-218
- Grünbaum, A., 1970, ‘Modern Science and Zeno's Paradoxes of Motion’, in
Salmon [1970], pp. 200-250
- Hawthorne, J., 2000, "Before-Effect and Zeno Causality", Nous,
34.4, pp. 622-633
- Hogarth, M. L., 1992, ‘Does General Relativity Allow an Observer to View
an Eternity in a Finite Time?’, Foundations of Physics Letters,
5, pp. 173-181
- Hogarth, M. L., 1994, ‘Non-Turing Computers and Non-Turing Computability’,
in PSA 1994, D. Hull, M. Forbes and R.M. Burian (eds.),
1, East Lansing: Philosophy of Science Association, pp.
126-138
- Holgate, P., 1994, ‘Discussion: Mathematical Notes on Ross's Paradox’,
British Journal for the Philosophy of Science, 45,
pp. 302-304
- Koetsier, T. and Allis, V., 1997, ‘Assaying Supertasks’, Logique &
Analyse, 159, pp. 291-313
- McLaughlin, W. I., 1998, ‘Thomson's Lamp is Dysfunctional’,
Synthese, 116, pp. 281-301
- Moore, A. W., 1989-90, ‘A Problem for Intuitionism: The Apparent
Possibility of Performing Infinitely Many Tasks in a Finite Time’,
Proceedings of the Aristotelian Society, 90, pp.
17-34
- Moore, A. W., 1990, The Infinite, London: Routledge
- Norton, J. D., 1999, ‘A Quantum Mechanical Supertask’, Foundations of
Physics, 29, pp. 1265-1302
- Owen, G. E. L., 1957-58, ‘Zeno and the Mathematicians’, Proceedings of
the Aristotelian Society, LVIII, pp. 199-222, reprinted
in Salmon [1970]
- Pérez Laraudogoitia, J., 1996, ‘A Beautiful Supertask’, Mind,
105, pp. 81-83
- Pérez Laraudogoitia, J., 1997, ‘Classical Particle Dynamics, Indeterminism
and a Supertask’, British Journal for the Philosophy of Science,
48, pp. 49-54
- Pérez Laraudogoitia, J., 1998, ‘Infinity Machines and Creation Ex
Nihilo’, Synthese, 115, pp. 259-265
- Pérez Laraudogoitia, J., 1998, ‘Some Relativistic and Higher Order
Supertasks’, Philosophy of Science, 65, pp. 502-517
- Pérez Laraudogoitia, J., 1999, ‘Earman and Norton on Supertasks that
Generate Indeterminism’, British Journal for the Philosophy of
Science, 50, pp.137-141
- Pérez Laraudogoitia, J., 1999, ‘Why Dynamical Self-excitation is
Possible’, Synthese, 119, pp. 313-323
- Pérez Laraudogoitia, J., 2001, "Indeterminism, classical gravitation and
non-collision singularities", International Studies in the Philosophy of
Science, 15.3, pp. 269-274
- Pérez Laraudogoitia, J., 2003, "Taking Self-excitations Seriously: On
Angel's Initial Condition", British Journal for the Philosophy of
Science, 54, pp.319-326
- Pitowsky, I., 1990, ‘The Physical Church Thesis and Physical Computational
Complexity’, Iyyun, 39, pp. 81-99
- Priest, G., 1982, ‘To Be and Not to Be: Dialectical Tense Logic’,
Studia Logica, XLI, pp. 157-176
- Ray, C., 1990, ‘Paradoxical Tasks’, Analysis,
50, pp. 71-74
- Ray, C., 1991, Time, Space and Philosophy, London: Routledge
- Sainsbury, R. M., 1988, Paradoxes, Cambridge: Cambridge
University Press
- Salmon, W., (ed.), 1970, Zeno's Paradoxes, Indianapolis:
Bobbs-Merril
- Salmon, W., 1980, Space, Time and Motion: A Philosophical
Introduction, Minneapolis: University of Minnesota Press
- Smith, J. W., 1986, Reason, Science and Paradox, London: Croom
Helm
- Sorabji, R., 1983, Time, Creation and the Continuum, London:
Gerald Duckworth and Co. Ltd.
- Svozil, K., 1993, Randomness and Undecidability in Physics,
Singapore: World Scientific
- Taylor, R., 1951-52, ‘Mr. Black on Temporal Paradoxes’, Analysis,
XII, pp. 38-44
- Taylor, R., 1952-53, ‘Mr. Wisdom on Temporal Paradoxes’,
Analysis, XIII, pp. 15-17
- Thomson, J., 1954-55, ‘Tasks and Super-Tasks’, Analysis,
XV, pp. 1-13; reprinted in Salmon [1970]
- Thomson, J., 1967, ‘Infinity in Mathematics and Logic’, in
Encyclopedia of Philosophy, P. Edwards (ed.), 4, New
York: MacMillan, pp. 183-90
- Thomson, J., 1970, ‘Comments on Professor Benacerraf's Paper’, in Salmon
[1970], pp. 130-38.
- Van Bendegem, J. P., 1994, ‘Ross' Paradox is an Impossible Super Task’,
British Journal for the Philosophy of Science, 45,
pp. 743-48
- Van Bendegem, J. P., 1995-1997, ‘In Defence of Discrete Space and Time’,
Logique & Analyse, 150-151-152, pp. 127-150
- Vlastos, G., 1966, ‘Zeno's Race Course’, Journal of the History of
Philosophy, IV, pp. 95-108
- Vlastos, G., 1967, ‘Zeno of Elea’, in Encyclopedia of Philosophy,
P. Edwards (ed.), 8, New York: MacMillan, pp.369-79
- Watling, J., 1953, ‘The Sum of an Infinite Series’, Analysis,
XIII, pp. 39-46
- Wedeking, G. A., 1968, ‘On a Finitist "Solution" to Some Zenonian
Paradoxes’, Mind, 77, pp. 420-26
- Weyl, H., 1949, Philosophy of Mathematics and Natural Science,
Princeton: Princeton University Press
- Whitrow, G. J., 1961, The Natural Philosophy of Time, Edinburgh:
Thomas Nelson & Sons
- Wisdom, J. O., 1951-52, ‘Achilles on a Physical Racecourse’,
Analysis, XII, pp. 67-72, reprinted in Salmon [1970]
[Please contact the author with
suggestions.]
infinity | space and time:
Malament-Hogarth spacetimes and the new computability | Zeno's paradoxes
A | B | C | D | E | F | G | H | I | J | K | L | M | N | O | P | Q | R | S | T | U | V | W | X | Y | Z
Stanford Encyclopedia of Philosophy




