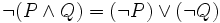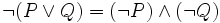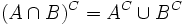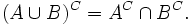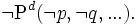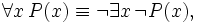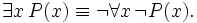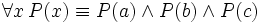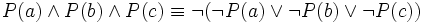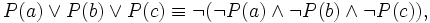Your continued donations keep Wikipedia running!

De Morgan's laws

From Wikipedia, the free encyclopedia

In logic, De Morgan's laws (or De Morgan's theorem) are rules in formal logic relating pairs of dual logical operators in a systematic manner expressed in terms of negation. The relationship so induced is called De Morgan duality.

To give some intuition, suppose P is true if and only if it is raining and Q is true if and only if you are wearing a raincoat. If you never go in the rain without a raincoat, then it can't be that P is true and Q is false. Thus, following formula is true:

not(P and (not Q))

On the other hand, another way of expressing the same statement is that either:

It's not raining, so you don't care whether you're wearing a raincoat or not;
You're wearing a raincoat, so you don't care whether it's raining or not.

In symbols, this would be written:

(not P) or Q

One of De Morgan's laws tells us that these two formulas are equivalent.

[edit]

History and formulations

Augustus De Morgan originally observed that in classical propositional logic the following relationships hold:

not (P and Q) = (not P) or (not Q)

not (P or Q) = (not P) and (not Q)

De Morgan's observation influenced the algebraisation of logic undertaken by George Boole, which cemented De Morgan's claim to the find, although a similar observation was made by Aristotle and was known to Greek and Medieval logicians (cf. Bocheński's History of Formal Logic).

In formal logic the laws are usually written

$\neg(P\wedge Q)=(\neg P)\vee(\neg Q)$

$\neg(P\vee Q)=(\neg P)\wedge(\neg Q)$

and in set theory

$(A\cap B)^C=A^C\cup B^C$

$(A\cup B)^C=A^C\cap B^C.$

In extensions of classical propositional logic, the duality still holds (that is, to any logical operator we can always find its dual), since in the presence of the identities governing negation, one may always introduce an operator that is the De Morgan dual of another. This leads to an important property of logics based on classical logic, namely the existence of negation normal forms: any formula is equivalent to another formula where negations only occur applied to the non-logical atoms of the formula. The existence of negation normal forms drives many applications, for example in digital circuit design, where it is used to manipulate the types of logic gates, and in formal logic, where it is a prerequisite for finding the conjunctive normal form and disjunctive normal form of a formula. Computer programmers use them to change a complicated statement like IF ... AND (... OR ...) THEN ... into its opposite. They are also often useful in computations in elementary probability theory.

Let us define the dual of any propositional operator P(p, q, ...) depending on elementary propositions p, q, ... to be

$\neg \mbox{P}^d(\neg p, \neg q, ...).$

This idea can be generalised to quantifiers, so for example the universal quantifier and existential quantifier are duals:

$\forall x \, P(x) \equiv \neg \exists x \, \neg P(x),$

$\exists x \, P(x) \equiv \neg \forall x \, \neg P(x).$

To relate these quantifier dualities to the De Morgan laws, set up a model with some small number of elements in its domain D, such as

D = {a, b, c}.

Then

$\forall x \, P(x) \equiv P(a) \wedge P(b) \wedge P(c)$

and

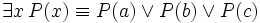$\exists x \, P(x) \equiv P(a) \vee P(b) \vee P(c)$ .

But, using De Morgan's laws,

$P(a) \wedge P(b) \wedge P(c) \equiv \neg (\neg P(a) \vee \neg P(b) \vee \neg P(c))$

and

$P(a) \vee P(b) \vee P(c) \equiv \neg (\neg P(a) \wedge \neg P(b) \wedge \neg P(c)),$

verifying the quantifier dualities in the model.

Then, the quantifier dualities can be extended further to modal logic, relating the box and diamond operators:

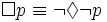$\Box p \equiv \neg \Diamond \neg p$ ,

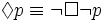$\Diamond p \equiv \neg \Box \neg p$ .

In its application to the alethic modalities of possibility and necessity, Aristotle observed this case, and in the case of normal modal logic, the relationship of these modal operators to the quantification can be understood by setting up models using Kripke semantics.

In the sense of computer science, in several languages (such as Java 1.5) De Morgan's laws can be simplified to:

!(p && q) is the same as !p || !q

!(p || q) is the same as !p && !q

In electrical engineering contexts, the negation operator can be written as an overline above the terms to be negated. Thus, electrical engineering students are often taught to remember DeMorgan's laws using the mnemonic "break the line, change the sign".

[edit]

Quotes

It should be noted that the contradictory opposite of a disjunctive proposition is a conjunctive proposition composed of the contradictories of the parts of the disjunctive proposition (William of Ockham, Summa Logicae).

[edit]