Double negative elimination

From Wikipedia, the free encyclopedia

In logic and the propositional logic, the inference rules double negative elimination (also called double negation elimination) and double negative introduction (also called double negation introduction) allow deriving the double negative equivalent by adding (for double negative introduction) or removing (for double negative elimination) a pair of negation signs. This is based on the equivalence of, for example,

It is not the case that it is not raining.

and

It is raining.

Formally, the rule double negative elimination is:

  ¬¬A
  ∴ A

Formally, the rule double negative introduction is:

  A      
  ∴ ¬¬A

The rule of double negative introduction states the converse, that double negatives can be added without changing the meaning of a proposition.

These two rules — double negative elimination and introduction — can be restated as follows (in sequent notation):

,

.

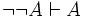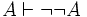Applying the Deduction Theorem to each of these two inference rules produces the pair of valid conditional formulas

,

,

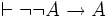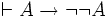which can be combined together into a single biconditional formula

.

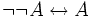Since biconditionality is an equivalence relation, any instance of ¬ ¬A in a well-formed formula can be replaced by A, leaving unchanged the truth-value of the wff.

Double negative elimination is a theorem of classical logic, but not intuitionistic logic. Because of the constructive flavor of intuitionistic logic, a statement such as It's not the case that it's not raining is weaker than It's raining. The latter requires a proof of rain, whereas the former merely requires a proof that rain would not be contradictory. (This distinction also arises in natural language in the form of litotes.) Double negation introduction is a theorem of intuitionistic logic, as is .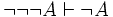

In set theory also we have the negation operation of the complement which obeys this property: a set A and a set (A^C)^C (where A^C represents the complement of A) are the same.