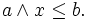Heyting algebra
From Wikipedia, the free encyclopedia
In mathematics, Heyting algebras are special partially ordered sets that constitute a generalization of Boolean algebras. Heyting algebras arise as models of intuitionistic logic, a logic in which the law of excluded middle does not in general hold. Complete Heyting algebras are a central object of study in pointless topology.
Contents |
Formal definitions
A Heyting algebra H is a bounded lattice such that for all a and b in H there is a greatest element x of H such that
This element is the relative pseudo-complement of a with
respect to b, and is denoted 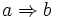 (or
(or
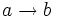 ).
).
An equivalent definition can be given by considering the mappings
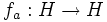 defined by
defined by 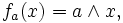
for some fixed a in H. A bounded lattice H is a Heyting
algebra iff all
mappings fa are the lower
adjoint of a monotone Galois connection. In
this case the respective upper adjoints ga are given by 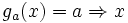 , where
, where
 is
defined as above.
is
defined as above.
A complete Heyting algebra is a Heyting algebra that is a complete lattice.
In any Heyting algebra, one can define the pseudo-complement  of some
element x by setting
of some
element x by setting 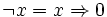 , where
0 is the least element of the Heyting algebra.
, where
0 is the least element of the Heyting algebra.
An element x of a Heyting algebra is called regular if 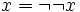 . An
element x is regular if and only if
. An
element x is regular if and only if 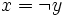 for
some element y of the Heyting algebra.
for
some element y of the Heyting algebra.
Properties
Heyting algebras are always distributive.
This is sometimes stated as an axiom, but in fact it follows from the existence
of relative pseudo-complements. The reason is that, being the lower adjoint of a
Galois connection, 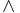 preserves
all existing suprema. Distributivity in turn
is just the preservation of binary suprema by
preserves
all existing suprema. Distributivity in turn
is just the preservation of binary suprema by 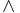 .
.
Furthermore, by a similar argument, the following infinite distributive law holds in any complete Heyting algebra:
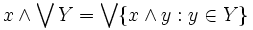
for any element x in H and any subset Y of H.
Not every Heyting algebra satisfies the two De Morgan laws. However, the following statements are equivalent for all Heyting algebras H:
- H satisfies both De Morgan laws.
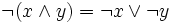 ,for
all
,for
all  .
.
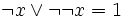 , for
all
, for
all 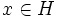 .
.
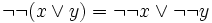 , for
all x, y in H.
, for
all x, y in H.
The pseudo-complement of an element x of H is the supremum of the
set 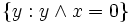 and it
belongs to this set (i.e.
and it
belongs to this set (i.e. 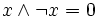 holds).
holds).
Boolean algebras are exactly those Heyting algebras in which 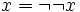 for all
x, or, equivalently, in which
for all
x, or, equivalently, in which 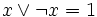 for all
x. In this case, the element
for all
x. In this case, the element 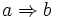 is
equal to
is
equal to 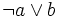 .
.
In any Heyting algebra, the least and greatest elements 0 and 1 are regular.
The regular elements of any Heyting algebra constitute a Boolean algebra. Unless all elements of the Heyting algebra are regular, this Boolean algebra will not be a sublattice of the Heyting algebra, because its join operation will be different.
Examples
- Every totally ordered set that
is a bounded lattice is also a Heyting algebra, where
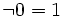 and
and
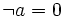 for
all a other than 0.
for
all a other than 0.
- Every Boolean algebra is a Heyting algebra, with p → q given by ¬p ∨ q.
- Every topology provides a complete
Heyting algebra in the form of its open set lattice. In this
case, the element
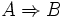 is
the interior of the
union of Ac and B,
where Ac denotes the
complement of the open set A. Not all complete Heyting algebras are of
this form. These issues are studied in pointless topology,
where complete Heyting algebras are also called frames or
locales.
is
the interior of the
union of Ac and B,
where Ac denotes the
complement of the open set A. Not all complete Heyting algebras are of
this form. These issues are studied in pointless topology,
where complete Heyting algebras are also called frames or
locales.
- The Lindenbaum algebra
of propositional intuitionistic
logic is a Heyting algebra. It is defined to be the set of all
propositional logic formulae, ordered via logical entailment: for any two
formulae F and G we have
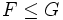 iff
iff
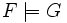 . At
this stage
. At
this stage 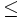 is
merely a preorder that induces a
partial order which is the desired Heyting algebra.
is
merely a preorder that induces a
partial order which is the desired Heyting algebra.
Heyting algebras as applied to intuitionistic logic
Arend Heyting (1898-1980) was himself interested in clarifying the foundational status of intuitionistic logic, in introducing this type of structure. The case of Peirce's law illustrates the semantic role of Heyting algebras. No simple proof is known that Peirce's law cannot be deduced from the basic laws of intuitionistic logic.
A Heyting algebra, from the logical standpoint, is essentially a
generalization of the usual system of truth values. Amongst other properties,
the largest element, called in logic 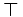 , is
analogous to 'true'. The usual two-valued logic system is the simplest example
of a Heyting algebra, one in which the elements of the algebra are
, is
analogous to 'true'. The usual two-valued logic system is the simplest example
of a Heyting algebra, one in which the elements of the algebra are 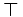 (true)
and
(true)
and 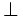 (false). That is, in abstract terms, the two-element Boolean algebra is also
a Heyting algebra.
(false). That is, in abstract terms, the two-element Boolean algebra is also
a Heyting algebra.
Classically valid formulas are those formulas that have a value of
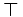 in this
Boolean algebra under any possible assignment of true and false to the formula's
variables — that is, they are formulas which are tautologies in the usual
truth-table sense. Intuitionistically valid formulas are those formulas
that have a value of
in this
Boolean algebra under any possible assignment of true and false to the formula's
variables — that is, they are formulas which are tautologies in the usual
truth-table sense. Intuitionistically valid formulas are those formulas
that have a value of 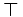 in
any Heyting algebra under any assignment of values to the formula's
variables.
in
any Heyting algebra under any assignment of values to the formula's
variables.
One can construct a Heyting algebra in which the value of Peirce's law is not
always 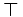 .
Consider the open sets of the Sierpinski space (the
simplest example of a Heyting algebra that is not Boolean) and observe that if
we interpret P by {1} and Q by
.
Consider the open sets of the Sierpinski space (the
simplest example of a Heyting algebra that is not Boolean) and observe that if
we interpret P by {1} and Q by 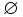 , then
the interpretation of Peirce's law ((P → Q) → P) → P is {1}, whereas
, then
the interpretation of Peirce's law ((P → Q) → P) → P is {1}, whereas 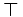 is
{0,1}. From what has just been said, this shows that it cannot be
intuitionistically derived. See Curry-Howard
isomorphism for the general context, of what this implies in type
theory.
is
{0,1}. From what has just been said, this shows that it cannot be
intuitionistically derived. See Curry-Howard
isomorphism for the general context, of what this implies in type
theory.
See also
References
- F. Borceux, Handbook of Categorical Algebra 3, In Encyclopedia of Mathematics and its Applications, Vol. 53, Cambridge University Press, 1994.
- G. Gierz, K.H. Hoffmann, K. Keimel, J. D. Lawson, M. Mislove and D. S. Scott, Continuous Lattices and Domains, In Encyclopedia of Mathematics and its Applications, Vol. 93, Cambridge University Press, 2003.