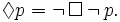Your continued donations keep Wikipedia running!

Modal logic

From Wikipedia, the free encyclopedia

Jump to: navigation, search

A modal logic is any logic for handling modalities: concepts like possibility, impossibility, and necessity. Logics for handling a number of other ideas, such as eventually, formerly, can, could, might, may, must are by extension also called modal logics, since it turns out that these can be treated in similar ways.

A formal modal logic represents modalities using modal sentential operators. For example, "Jones's murder was a possibility"; "Jones was possibly murdered"; and "It is possible that Jones was murdered," all contain the notion of possibility; in a modal logic this is represented as an operator, Possibly, attaching to the sentence Jones was murdered.

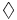The basic modal operators are usually $\Box$ (or L) for Necessarily and $\Diamond$ (or M) , for Possibly. They are defined in terms of one another this way:

$\Diamond p = \lnot\, \Box\, \lnot\, p.$

Thus it is possible that Jones was murdered if and only if it is not necessary that Jones was not murdered.

Contents

Alethic modalities

Necessity and possibility are sometimes called alethic modalities, from the Greek aletheia, truth. Modal logic was first developed to deal with these concepts, and only afterward was extended to others. For this reason, or perhaps for their familiarity and simplicity, necessity and possibility are often casually treated as the subject matter of modal logic.

A sentence is said to be

possible if it might be true (regardless of whether it is or is not actually true);
necessary if it could not possibly be false;
contingent if it is actually true, but not necessarily true. It could have been otherwise, so it is possibly true, and possibly false.

Thus if something is necessarily true, then it is true; if it is true, then it is possible.

Logical necessity

There are a number of different alethic modalities: logical possibility is, perhaps, the weakest, since almost anything intelligible is logically possible: Possibly, pigs can fly, Elvis is still alive, and the atomic theory of matter is false.

Likewise, almost nothing is logically impossible: something logically impossible is called a contradiction or a logical falsehood. It is possible that Elvis is alive; but it is impossible that Elvis is alive and is not alive. Many logicians also hold that mathematical truths are logically necessary: it is impossible that 2+2 ≠ 4.

Something which is logically necessary is called a logical truth. For example, it is necessary that if Elvis is alive, then he is alive. (Logical truths tend to look trivial like this.)

Physical possibility

Something is physically possible if it is permitted by the laws of nature. For example, it is possible for there to be an atom with an atomic number of 150, though there may not in fact be one. On the other hand, it is not possible, in this sense, for there to be an element whose nucleus contains cheese. While it is logically possible to travel faster than the speed of light, it is not, according to modern science, physically possible.

Metaphysical possibility

Philosophers ponder the properties objects have independently of those dictated by scientific laws. For example, it might be metaphysically necessary, as some have thought, that all thinking beings have bodies and can experience the passage of time, or that God exists (or does not exist). Saul Kripke has argued that every person necessarily has the parents they do have: anyone with different parents wouldn't be the same person.

Metaphysical possibility is generally thought to be stronger than bare logical possibility (fewer things are possible). Its exact relation to physical possibility is a matter of some dispute. Philosophers also disagree over whether metaphysical truths are necessary merely "by definition", or whether they reflect some underlying deep facts about the world, or something else entirely.

Confusion with epistemic modalities

Alethic modalities and epistemic modalities (see below) are often expressed in English using the same words. Thus, "It is possible that bigfoot exists" might mean either It would be possible for such a creature as a bigfoot to exist, or (more likely), "As far as I know, there may be some bigfoots."

In the former case, the speaker might know that there are not any bigfoots, but is saying that (unlike round squares), there could be some--the existence of bigfoot is not impossible. In the latter case he is saying that there may well be some right now.

Epistemic logic

Epistemic modalities (from the Greek episteme, knowledge), deal with the certainty of sentences. The operators are translated as "It is certainly true that..." and "It may (given the available information) be true that..." In ordinary speech both modalities are often expressed in similar words; the following contrasts may help:

A person, Jones, might reasonably say both: (1) "No, it is not possible that Bigfoot exists; I am quite certain of that;" and, (2) "Sure, Bigfoot possibly could exist." What Jones means by (1) is that given all the available information, there is no question remaining as to whether Bigfoot exists. This is an epistemic claim. By (2) he means that things might have been otherwise. He does not mean "it is possible that Bigfoot exists--for all I know." (So he is not contradicting (1).) Rather, he is making the metaphysical claim that it's possible for Bigfoot to exist, even though he doesn't.

From the other direction, Jones might say, (3) "It is possible that Goldbach's conjecture is true; but also possible that it is false," and also (4) "if it is true, then it is necessarily true, and not possibly false." Here Jones means that it is epistemically possible that it is true or false, for all he knows (Goldbach's conjecture has not been proven either true or false). But if there is a proof (heretofore undiscovered), then that would show that it is not logically possible for Goldbach's conjecture to be false—there could be no set of numbers that violated it. Logical possibility is a form of alethic possibility; (4) makes a claim about whether it is possible for a mathematical truth to have been false, but (3) only makes a claim about whether it is possible that the mathematical claim turns out false, for all Jones knows, and so again Jones does not contradict himself.

Epistemic possibilities also bear on the actual world in a way that metaphysical possibilities do not. Metaphysical possibilities bear on ways the world might have been, but epistemic possibilities bear on the way the world may be (for all we know). Suppose, for example, that I want to know whether or not to take an umbrella before I leave. If you tell me "It is possible that it is raining outside"--in the sense of epistemic possibility--then that would weigh on whether or not I take the umbrella. But if you just tell me that "It is possible for it to rain outside"--in the sense of metaphysical possibility--then I am no better off for this bit of modal enlightenment.

Temporal logic

There are several analogous modes of speech, which though less likely to be confused with alethic modalities are still closely related. One is talk of time. It seems reasonable to say that possibly it will rain tomorrow, and possibly it won't; on the other hand, if it rained yesterday, if it really already did so, then it cannot be quite correct to say "It may not have rained yesterday." It seems the past is "fixed," or necessary, in a way the future is not.

A standard method for formalizing talk of time is to use two pairs of operators, one for the past and one for the future. For the past, let "It has always been the case that . . ." be equivalent to the box, and let "It was once the case that . . ." be equivalent to the diamond. For the future, let "It will always be the case that . . ." be equivalent to the box, and let "it will eventually be the case that . . ." (If these two systems are used together, it will, obviously, be necessary to indicate, as by subscripts, which box is which.)

Deontic logic

Likewise talk of morality, or of obligation and norms generally, seems to have a modal structure. The difference between "You must do this" and "You may do this" looks a lot like the difference between "This is necessary and this is possible." Such logics are called deontic, from the Greek for "duty".

Other modal logics

Significantly, modal logics can be developed to accommodate most of these idioms; it is the fact of their common logical structure (the use of "intensional" or non-truth-functional sentential operators) that make them all varieties of the same thing. Epistemic logic is arguably best captured in the system "S4" ; deontic logic in the system "D", temporal logic in "t" (sic:lowercase) and alethic logic arguably with "S5".

Interpretations of modal logic

In the most common interpretation of modal logic, one considers "all logically possible worlds". If a statement is true in all possible worlds, then it is a necessary truth. If a statement happens to be true in our world, but is not true in all possible worlds, then it is a contingent truth. A statement that is true in some possible world (not necessarily our own) is called a possible truth.

Whether this "possible worlds idiom" is the best way to interpret modal logic, and how literally this idiom can be taken, is a live issue for metaphysicians. For example, the possible worlds idiom would translate the claim about Bigfoot as "There is some possible world in which Bigfoot exists". To maintain that Bigfoot's existence is possible, but not actual, one could say, "There is some possible world in which Bigfoot exists; but in the actual world, Bigfoot does not exist". But it is unclear what it is that making modal claims commits us to. Are we really alleging the existence of possible worlds, every bit as real as our actual world, just not actual? David Lewis infamously bit the bullet and said yes, possible worlds are as real as our own. This position is called "modal realism". Unsurprisingly, most philosophers are unwilling to sign on to this particular doctrine, seeking alternate ways to paraphrase away the apparent ontological commitments implied by our modal claims.

Formal rules

There are many modal logics, with many different properties. In many of them the concepts of necessity and possibility satisfy the following de Morganesque relationship:

"It is not necessary that X" is equivalent to "It is possible that not X".

"It is not possible that X" is equivalent to "It is necessary that not X".

However modal logic texts like Hughes and Cresswell's "A New Introduction to Modal Logic" cover some systems where this isn't true.

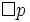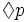Modal logic adds to the well formed formulae of propositional logic operators for necessity and possibility. In some notations "necessarily p" is represented using a "box" ( $\Box p$ ), and "possibly p" is represented using a "diamond" ( $\Diamond p$ ). Whatever the notation, the two operators are definable in terms of each other:

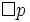$\Box p$ (necessarily p) is equivalent to 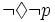$\neg \Diamond \neg p$ (not possible that not-p)
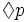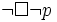$\Diamond p$ (possibly p) is equivalent to $\neg \Box \neg p$ (not necessarily not-p)

Hence, the $\Box$ and 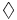$\Diamond$ are called dual operators.

Precisely what axioms must be added to propositional logic to create a usable system of modal logic has been the subject of much debate. One weak system, named K after Saul Kripke, adds only the following to a classical axiomatization of propositional logic:

Necessitation Rule: If p is a theorem of K, then so is $\Box p$ .
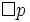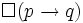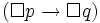Distribution Axiom: If $\Box (p \rightarrow q)$ then $(\Box p \rightarrow \Box q)$ (this is also known as axiom K)

These rules lack an axiom to go from the necessity of p to p actually being the case, and therefore are usually supplemented with the following "reflexivity" axiom, which yields a system often called T.

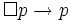$\Box p \rightarrow p$ (If it's necessary that p, then p is the case)

This is a rule of most, but not all modal logic systems. Jay Zeman's book "Modal Logic" covers systems like S1^0 that don't have this rule.

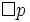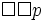K is a weak modal logic, however. In particular, it leaves it open that a proposition be necessary but only contingently necessary. That is, it is not a theorem of K that if $\Box p$ is true then $\Box \Box p$ is true, i.e., that necessary truths are necessarily necessary. This may not be a great defect for K, since these seem like awfully strange questions and any attempt to answer them involves us in confusing issues. In any case, different solutions to questions such as these produce different systems of modal logic.

The system most commonly used today is modal logic S5, which robustly answers the questions by adding axioms which make all modal truths necessary: for example, if it's possible that p, then it's necessarily possible that p, and if it's necessary that p it's also necessary that it's necessary. This has been thought by many to be justified on the grounds that it is the system which is obtained when we demand that every possible world is possible relative to every other world. Nevertheless, other systems of modal logic have been formulated, in part, because S5 may not be a good fit for every kind of metaphysical modality of interest to us. (And if so, that may mean that possible worlds talk is not a good fit for these kinds of modality either.)

Development of modal logic

Although Aristotle's logic is almost entirely concerned with the theory of the categorical syllogism, his work also contains some extended arguments on points of modal logic (such as his famous Sea-Battle Argument in De Interpretatione § 9) and their connection with potentialities and with time. Following on his works, the Scholastics developed the groundwork for a rigorous theory of modal logic, mostly within the context of commentary on the logic of statements about essence and accident. Among the medieval writers, some of the most important works on modal logic can be found in the works of William of Ockham and John Duns Scotus.

The founder of formal modal logic is C. I. Lewis, who introduced a system (later called S3) in his monograph A Survey of Symbolic Logic (1918) and (with C. H. Langford) the systems S1-S5 in the book Symbolic Logic (1932). J. C. C. McKinsey used algebraic methods (Boolean algebras with operators) to prove the decidability of Lewis' S2 and S4 in 1941. Saul Kripke devised the relational semantics or possible worlds semantics for modal logics starting in 1959. Vaughan Pratt introduced dynamic logic in 1976. Amir Pnueli proposed the use of temporal logic to formalise the behaviour of continually operating concurrent programs in 1977.

Temporal logic, originated by A. N. Prior in 1957, is closely related to modal logic, as adding modal operators [F] and [P], meaning, respectively, henceforth and hitherto, leads to a system of temporal logic.

Flavours of modal logics include: propositional dynamic logic (PDL), propositional linear temporal logic (PLTL), linear temporal logic (LTL), computational tree logic (CTL), Hennessy-Milner logic, S1-S5, and T.

A note about intensionality of modal logics

Some people argue that modal logics are characterized by semantic intensionality: the truth value of a complex formula cannot be determined by the truth values of its subformulae, and modal operators cannot be formalized by an extensional semantics: both "George W. Bush is President of the United States" and "2 + 2 = 4" are true, yet "Necessarily, George W. Bush is President of the United States" is false, while "Necessarily, 2 + 2 = 4" is true.

Actually, this claim is not correct, since we can give the semantics of a modal logic by structural induction, if we use stateful models, also called coalgebraic models. For example, we can consider the following very simple modal logic syntax:

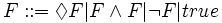
$F ::= \Diamond F | F \land F | \lnot F | true$

We can derive dual connectives using the basic ones:

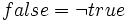
$false = \lnot true$

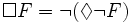
$\Box F = \lnot (\Diamond \lnot F)$

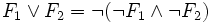
$F_1 \lor F_2 = \lnot (\lnot F_1 \land \lnot F_2)$

The truth value of a formula is defined over models that are not sets, but transition systems.

A transition system is a pair $(S, T)$ where $S$ is a set and 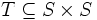$T \subseteq S \times S$ .

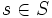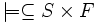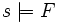The interpretation of the logic over the state $s \in S$ , given a transition system $(S, T)$ , is a relation $\models \subseteq S \times F$ , where $s \models F$ is read "the state s satisfies the formula F", given by structural induction as follows:

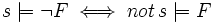
$s \models \lnot F \iff not\,s \models F$

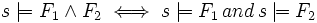
$s \models F_1 \land F_2 \iff s \models F_1\, and\, s \models F_2$

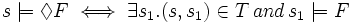
$s \models \Diamond F \iff \exists s_1 . (s,s_1) \in T \, and\, s_1 \models F$

If we view a transition system $(S, T)$ as a set $S$ of states and a set $T$ of transitions from a state to another, the modal formula 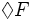$\Diamond F$ , which is called the "next" modality, is read as "in my possible next states, there is one that satisfies F".

This logic is too simple for practical uses; more complicated logics can have more complicated models (an example being Kripke frames), however the definition of the semantics is usually given by structural induction over states.

References

Patrick Blackburn, Maarten de Rijke, and Yde Venema (2001) "Modal Logic". Cambridge University Press.
Aleksander Chagrov and Michael Zakharyaschev (1997) "Modal Logic". Oxford University Press.
Brian F. Chellas (1980) "Modal Logic: an introduction". Cambridge University Press.
M. Fitting and R.L. Mendelsohn (1998) First Order Modal Logic. Kluwer Academic Publishers.
James Garson (2003) Modal logic. Entry in the Stanford Encyclopedia of Philosophy.
Rod Girle (2000) Modal Logics and Philosophy. Acumen (UK). The proof theory employs refutation trees (semantic tableaux). A good introduction to the varied interpretations of modal logic.
Robert Goldblatt (1992) "Logics of Time and Computation", CSLI Lecture Notes No. 7, Centre for the Study of Language and Information, Stanford University, 2nd ed. (distributed by University of Chicago Press).
Robert Goldblatt (1993) "Mathematics of Modality", CSLI Lecture Notes No. 43, Centre for the Study of Language and Information, Stanford University. (distributed by University of Chicago Press).
G.E. Hughes and M.J. Cresswell (1968) An Introduction to Modal Logic, Methuen.
G.E. Hughes and M.J. Cresswell (1984) A Companion to Modal Logic, Medhuen.
G.E. Hughes and M.J. Cresswell (1996) A New Introduction to Modal Logic, Routledge.
E.J. Lemmon (with Dana Scott), 1977, An Introduction to Modal Logic, American Philosophical Quarterly Monograph Series, no. 11 (ed. by Krister Segerberg), Basil Blackwell, Oxford.
J. Jay Zeeman (1973) Modal Logic. D. Reidel Publishing Company.

See also

External links

A discussion of modal logic by John McCarthy
Bibliography of Non-Standard Logics by Peter Suber
List of Logic Systems List of most of the more popular modal logics.
Advances in Modal Logic (bi-annual international conference and book series in Modal Logic)
Basic Concepts in Modal Logic (pdf) by Edward N. Zalta

Acknowledgements

This article contains some material originally from the Free On-line Dictionary of Computing which is used with permission under the GFDL.

Retrieved from "http://en.wikipedia.org/wiki/Modal_logic"

Categories: Logic | Modal logic

Views

Personal tools

Sign in / create account

Search

Toolbox

In other languages