Your continued donations keep Wikipedia running!

Model theory

From Wikipedia, the free encyclopedia

This article discusses model theory as a mathematical discipline and not the informally used term mathematical model as used in other parts of mathematics and science.

In mathematics, model theory is the study of the representation of mathematical concepts in terms of set theory, or the study of the models which underlie mathematical systems. It assumes that there are some pre-existing mathematical objects out there, and asks questions regarding how or what theorems can be proven given the objects, some operations or relations amongst the objects, and a set of axioms.

The independence of the axiom of choice and the continuum hypothesis from the other axioms of set theory (proved by Paul Cohen and Kurt Gödel) are the two most famous results arising from model theory. It was proved that both the axiom of choice and its negation are consistent with the Zermelo-Fraenkel axioms of set theory; the same result holds for the continuum hypothesis. These results are applications of model-theoretic methods to axiomatic set theory.

An example of the concepts of model theory is provided by the theory of the real numbers. We start with a set of individuals, where each individual is a real number, and a set of relations and/or functions, such as { ×, +, −, ., 0, 1 }. If we ask a question such as "∃y (y × y = 1 + 1)" in this language, then it is clear that the sentence is true for the reals - there is such a real number y, namely the square root of 2; for the rational numbers, however, the sentence is false. A similar proposition, "∃y (y × y = 0 − 1)", is false in the reals, but is true in the complex numbers, where i × i = 0 − 1.

[edit]

Definition

A model, or structure, is formally defined in the context of some language L, which consists of a set of constant symbols, a set of relation symbols, and a set of function symbols. A model of the language L consists of several things:

A universe set A which contains all the objects of interest (the "domain of discourse"), and
An element of A for each constant symbol of L.
A function from Aⁿ to A for each function symbol of L of valence n.
An n-ary relation on A (in other words a subset of Aⁿ) for each predicate (or relation) of L of valence n.

The "valence" of functions or relations is sometimes also referred to as the arity (a back-formation from the terms "unary," "binary," "ternary," or "n-ary").

A theory is defined as a set of sentences in the language L, and is called a closed theory if the set of sentences is closed under the usual rules of inference. For example, the set of all sentences true in some particular model (e.g. the reals) is a closed theory. A model of the theory T consists of a model over the language L in which all sentences of the theory T are true, normally defined by means of a T-schema.

A theory is said to be satisfiable if it has a model.

For example, the language of partial orders has just one binary relation ≥. So a model of the language of partial orders is just a set with a binary relation denoted by ≥, and it is a model of the theory of partial orders if in addition it satisfies the axioms of a partial order.

[edit]

Theorems of model theory

Gödel's completeness theorem (not to be confused with his incompleteness theorems) says that a theory has a model if and only if it is consistent, i.e. no contradiction is proved by the theory. This is the heart of model theory as it lets us answer questions about theories by looking at models and vice-versa. One should not confuse the completeness theorem with the notion of a complete theory. A complete theory is a theory which contains every sentence or its negation. Importantly, one can find a complete consistent theory extending any consistent theory. However, as shown by Gödel's incompleteness theorems only in relatively simple cases will it be possible to have a complete consistent theory that is also recursive, i.e. that can be described by a recursively enumerable set of axioms. In particular, the theory of natural numbers has no recursive complete and consistent theory. Non-recursive theories are of little practical use, since it is undecidable if a proposed axiom is indeed an axiom, making proof-checking practically impossible.

The compactness theorem states that a set of sentences S is satisfiable if every finite subset of S is satisfiable. In the context of proof theory the analogous statement is trivial, since every proof can have only a finite number of antecedents used in the proof; in the context of model theory, however, this proof is somewhat more difficult. There are two well known proofs, one by Gödel (which goes via proofs) and one by Malcev (which is more direct and allows us to restrict the cardinality of the resulting model).

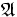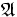Model theory is usually concerned with first-order logic, and many important results (such as the completeness and compactness theorems) fail in second-order logic or other alternatives. In first-order logic all infinite cardinals look the same to a language which is countable. This is expressed in the Löwenheim-Skolem theorems, which state that any theory with an infinite model $\mathfrak{A}$ has models of all infinite cardinalities (at least that of the language) which agree with $\mathfrak{A}$ on all sentences, i.e. they are 'elementarily equivalent'.

So in particular, set theory (which is expressed in a countable language) has a countable model; this is known as Skolem's paradox, since there are sentences in set theory which postulate the existence of uncountable sets and yet these sentences are true in our countable model. Particularly the proof of the independence of the continuum hypothesis requires considering sets in models which appear to be uncountable when viewed from within the model, but are countable to someone outside the model.

[edit]

References

Wilfrid Hodges, A shorter model theory (1997) Cambridge University Press ISBN 0-521-58713-1
Wilfrid Hodges, Model theory (1993) Cambridge University Press.
C. C. Chang, H. J. Keisler Model theory (1977) ISBN 0720406927
David Marker Model Theory: An Introduction (2002) Springer-Verlag, ISBN 0387987606