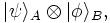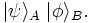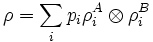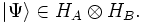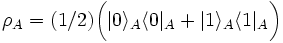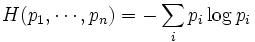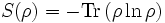Your continued donations keep Wikipedia running!

Quantum entanglement

From Wikipedia, the free encyclopedia

Quantum entanglement is a quantum mechanical phenomenon in which the quantum states of two or more objects have to be described with reference to each other, even though the individual objects may be spatially separated. This leads to correlations between observable physical properties of the systems. For example, it is possible to prepare two particles in a single quantum state such that when one is observed to be spin-up, the other one will always be observed to be spin-down and vice versa, this despite the fact that it is impossible to predict, according to quantum mechanics, which set of measurements will be observed. As a result, measurements performed on one system seem to be instantaneously influencing other systems entangled with it. Quantum entanglement does not enable the transmission of classical information faster than the speed of light (see discussion in next section below).

Quantum entanglement is closely concerned with the emerging technologies of quantum computing and quantum cryptography, and has been used to experimentally realize quantum teleportation. At the same time, it prompts some of the more philosophically oriented discussions concerning quantum theory. The correlations predicted by quantum mechanics, and observed in experiment, reject the principle of local realism, which is that information about the state of a system should only be mediated by interactions in its immediate surroundings. Different views of what is actually occurring in the process of quantum entanglement can be related to different interpretations of quantum mechanics.

[edit]

Background

Entanglement is one of the properties of quantum mechanics which caused Einstein and others to dislike the theory. In 1935, Einstein, Podolsky, and Rosen formulated the EPR paradox, a quantum-mechanical thought experiment with a highly counterintuitive and apparently nonlocal outcome. Einstein famously derided entanglement as "spooky action at a distance."

On the other hand, quantum mechanics has been highly successful in producing correct experimental predictions, and the strong correlations associated with the phenomenon of quantum entanglement have in fact been observed. One apparent way to explain quantum entanglement is an approach known as "hidden variable theory", in which unknown deterministic microscopic parameters would cause the correlations. However, in 1964 Bell derived an upper limit, known as Bell's inequality, on the strength of correlations for any theory obeying "local realism" (see principle of locality). Quantum entanglement can lead to stronger correlations that violate this limit, so that quantum entanglement is experimentally distinguishable from a broad class of local hidden-variable theories. Results of subsequent experiments have overwhelmingly supported quantum mechanics. It is known that there are a number of loopholes in these experiments. High efficiency and high visibility experiments are now in progress which should accept or reject those loopholes. For more information, see the article on Bell test experiments.

Observations on entangled states naively appear to conflict with the property of Einsteinian relativity that information cannot be transferred faster than the speed of light. Although two entangled systems appear to interact across large spatial separations, no useful information can be transmitted in this way, so causality cannot be violated through entanglement. This occurs for two subtle reasons: (i) quantum mechanical measurements yield probabilistic results, and (ii) the no cloning theorem forbids the statistical inspection of entangled quantum states.

Although no information can be transmitted through entanglement alone, it is possible to transmit information using a set of entangled states used in conjunction with a classical information channel. This process is known as quantum teleportation. Despite its name, quantum teleportation cannot be used to transmit information faster than light, because a classical information channel is involved.

[edit]

Formalism

The following discussion builds on the theoretical framework developed in the articles bra-ket notation and mathematical formulation of quantum mechanics.

Consider two noninteracting systems $A$ and $B$ , with respective Hilbert spaces $H A$ and $H B$ . The Hilbert space of the composite system is the tensor product

$H_A \otimes H_B$

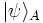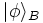If the first system is in state $| \psi \rangle_A$ and the second in state $| \phi \rangle_B$ , the state of the composite system is

$|\psi\rangle_A \otimes |\phi\rangle_B,$

which is often also written as

$|\psi\rangle_A \; |\phi\rangle_B.$

States of the composite system which can be represented in this form are called separable states, or product states.

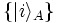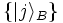Pick observables (and corresponding Hermitian operators) $Ω A$ acting on $H A$ , and $Ω B$ acting on $H B$ . According to the spectral theorem, we can find a basis $\{|i \rangle_A\}$ for $H A$ composed of eigenvectors of $Ω A$ , and a basis $\{|j \rangle_B\}$ for $H B$ composed of eigenvectors of $Ω B$ . We can then write the above pure state as

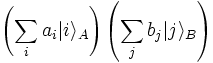$\left( \sum_i a_i |i\rangle_A \right) \left( \sum_j b_j |j\rangle_B \right)$ ,

for some choice of complex coefficients $a i$ and $b j$ . This is not the most general state of 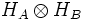$H_A \otimes H_B$ , which has the form

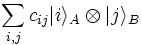$\sum_{i,j} c_{ij} |i\rangle_A \otimes |j\rangle_B$ .

If such a state is not separable, it is known as an entangled state.

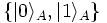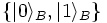For example, given two basis vectors $\{|0\rangle_A, |1\rangle_A\}$ of $H A$ and two basis vectors $\{|0\rangle_B, |1\rangle_B\}$ of $H B$ , the following is an entangled state:

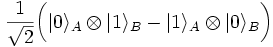${1 \over \sqrt{2}} \bigg( |0\rangle_A \otimes |1\rangle_B - |1\rangle_A \otimes |0\rangle_B \bigg)$ .

If the composite system is in this state, it is impossible to attribute to either system $A$ or system $B$ a definite pure state. Instead, their states are superposed with one another. In this sense, the systems are "entangled".

Now suppose Alice is an observer for system $A$ , and Bob is an observer for system $B$ . If Alice performs the measurement $Ω A$ , there are two possible outcomes, occurring with equal probability:

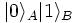
Alice measures $0$ , and the state of the system collapses to $|0\rangle_A |1\rangle_B$
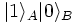Alice measures $1$ , and the state of the system collapses to $|1\rangle_A |0\rangle_B$ .

If the former occurs, any subsequent measurement of $Ω B$ performed by Bob always returns $1$ . If the latter occurs, Bob's measurement always returns $0$ . Thus, system $B$ has been altered by Alice performing her measurement on system $A$ ., even if the systems $A$ and $B$ are spatially separated. This is the foundation of the EPR paradox.

The outcome of Alice's measurement is random. Alice cannot decide which state to collapse the composite system into, and therefore cannot transmit information to Bob by acting on her system. (There is a possible loophole: if Bob could make multiple duplicate copies of the state he receives, he could obtain information by collecting statistics. This loophole is closed by the no cloning theorem, which forbids the creation of duplicate states.) Causality is thus preserved, as claimed above.

[edit]

Ensembles

As mentioned above, a state of a quantum system is given by a unit vector in a Hilbert space. More generally, if one has a large number of copies of the same system, then the state of this ensemble is described by a density matrix, which is a positive matrix (or trace class, when the state space is infinite dimensional) and has trace 1. Again, by the spectral theorem, such a matrix takes the general form:

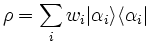$\rho = \sum_i w_i |\alpha_i\rangle \langle\alpha_i|$ ,

where the $w i$ 's sum up to 1 (in the infinite dimensional case, we would take the closure of such states in the trace norm). We can interpret $ρ$ as representing an ensemble where $w i$ is the proportion of the ensemble whose states are 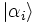$|\alpha_i\rangle$ . When a mixed state has rank 1, it therefore describes a pure ensemble. When there is less than total information about the state of a quantum system we need density matrices to represent the state (see experiment discussed below).

Following the definition in previous section, for a bipartite composite system, mixed states are just density matrices on 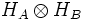$H_A \otimes H_B$ . Extending the definition of separability from the pure case, we say that a mixed state is separable if it can be written as

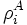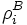$\rho = \sum_i p_i \rho_i^A \otimes \rho_i^B$

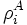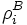,where $\rho_i^A$ 's and $\rho_i^B$ 's are they themselves states on the subsystems A and B respectively. In other words, a state is separable if it is probability distribution over uncorrelated states, or product states. We can assume without loss of generality that $\rho_i^A$ and $\rho_i^B$ are pure ensembles. A state is then said to be entangled if it is not separable. In general, finding out whether or not a mixed state is entangled is considered difficult. Formally, it has been shown to be NP-hard. For the $2 \times 2$ and $2 \times 3$ cases, a necessary and sufficient criterion for separability is given by the famous PPT (Positve Partial Transpose) condition.

Experimentally, a mixed ensemble might be realized as follows. Consider a "black-box" apparatus that spits electrons towards an observer. The electrons' Hilbert spaces are identical. The apparatus might produce electrons that are all in the same state; in this case, the electrons received by the observer are then a pure ensemble. However, the apparatus could produce electrons in different states. 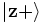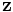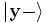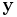For example, it could produce two populations of electrons: one with state $|\mathbf{z}+\rangle$ (spins aligned in the positive $\mathbf{z}$ direction), and the other with state $|\mathbf{y}-\rangle$ (spins aligned in the negative $\mathbf{y}$ direction.) Generally, there can be any number of populations, each corresponding to a different state. Therefore we now have a mixed ensemble.

[edit]

Reduced Density Matrices

Consider as above systems $A$ and $B$ each with a Hilbert space $H A$ , $H B$ . Let the state of the composite system be

$|\Psi \rangle \in H_A \otimes H_B.$

As indicated above, in general there is no way to associate a pure state to the component system $A$ . However, it still is possible to associate a density matrix. Let

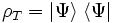$\rho_T = |\Psi\rangle \; \langle\Psi|$ .

which is the projection operator onto this state. The state of $A$ is the partial trace of $ρ T$ over the basis of system $B$ :

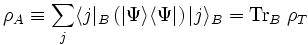$\rho_A \equiv \sum_j \langle j|_B \left( |\Psi\rangle \langle\Psi| \right) |j\rangle_B = \hbox{Tr}_B \; \rho_T$ .

$ρ A$ is sometimes called the reduced density matrix of $ρ$ on subsystem A. Colloquially, we "trace out" system B to obtain the reduced density matrix on A.

For example, the density matrix of $A$ for the entangled state discussed above is

$\rho_A = (1/2) \bigg( |0\rangle_A \langle 0|_A + |1\rangle_A \langle 1|_A \bigg)$

This demonstrates that that, as expected, the reduced density matrix for an entangled pure ensemble is a mixed ensemble. Also not surprisingly, the density matrix of $A$ for the pure product state 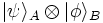$|\psi\rangle_A \otimes |\phi\rangle_B$ discussed above is

$\rho_A = |\psi\rangle_A \langle\psi|_A$ .

[edit]

Entropy

In this section we briefly discuss entropy of a mixed state and how it can be viewed as a measure of entanglement.

In classical information theory, to a probability distribution $p_1, \cdots, p_n$ , one can associate the Shannon entropy:

$H(p_1, \cdots, p_n ) = - \sum_i p_i \log p_i$

,where the logarithm is taken in base 2.

Since one can think of a mixed state ρ as a probability distribution over an ensemble, this leads naturally to the definition of the von Neumann entropy:

$S(\rho) = - \hbox{Tr} \left( \rho \ln{\rho} \right)$

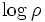,where the logarithm is again taken in base 2. In general, to calculate $\; \log \rho$ , one would use the Borel functional calculus. If ρ acts on a finite dimensional Hilbert space and has eigenvalues $\lambda_1, \cdots, \lambda_n$ , then we recover the Shannon entropy:

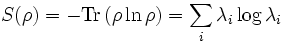$S(\rho) = - \hbox{Tr} \left( \rho \ln{\rho} \right) = \sum_i \lambda_i \log \lambda_i$ .

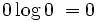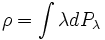Since an event of probability 0 should not contribute to the entropy, we adopt the convention that $0 \log 0 \; = 0$ . This extends to the infinite dimensional case as well: if ρ has spectral resolution $\rho = \int \lambda d P_{\lambda}$ , then we assume the same convention when calculating

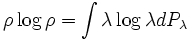$\rho \log \rho = \int \lambda \log \lambda d P_{\lambda}$ .

Entropy provides one tool which can be used to quantify entanglement (although other entanglement measures exist). As in statistical mechanics, one can say that the more uncertainty (number of microstates) possessed by the system, the larger the entropy. For example, the entropy of any pure state is zero, which is unsurprising since there is no uncertainty about a system in a pure state. The entropy of any of the two subsystems of the entangled state discussed above is $ln2$ (which can be shown to be the maximum entropy for $2 \times 2$ mixed states). If the overall system is pure, the entropy of one subsystem can be used to measure its degree of entanglement with the other subsystems. It turns out that, for pure states, the von Neumann entropy of reduced states is the unique measure of entanglement. On the other hand, uniqueness does not hold for mixed states. Physically speaking, this is because the uncertainty in the mixed state gives us entropy in itself, irrespective of whether or not the state is entangled.

As mentioned above, the information-theoretic definition is closely related to entropy in the sense of statistical mechanics (comparing the two definitions, we note that, in the present context, it is customary to set the Boltzmann constant $k = 1$ ). For example, by properties of the Borel functional calculus, we see that for any unitary operator U,

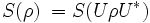$S(\rho) \; = S(U \rho U^*)$ .

Indeed, without the above property, the von Neumann entropy would not be well-defined. In particular, U could be the the time evolution operator of the system, i.e. 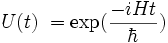$U(t) \; = \exp (\frac{-i H t }{\hbar})$ , where H is the Hamiltonian of the system. This associates the reversibility of a process with its resulting entropy change, i.e. a process is reversible if and only if it leaves the entropy of the system invariant. This provides a connection between quantum information theory and thermodynamics.

[edit]

Applications of entanglement

Entanglement has many applications in quantum information theory. Mixed state entanglement can be viewed as a resource for quantum communication. Among the most well known such applications of entanglement are superdense coding and quantum state teleportation(also called entanglement-assisted teleportation). Efforts to quantify this resource are often termed entanglement theory. See for example Entanglement Theory Tutorials.

The Reeh-Schlieder theorem of quantum field theory is sometimes seen as the QFT analogue of Quantum entanglement.

[edit]

References

M. Horodecki, P. Horodecki, R. Horodecki, Separability of Mixed States: Necessary and Sufficient Conditions, Physics Letters A 210, 1996.

L. Gurvits, Classical deterministic complexity of Edmonds' Problem and quantum entanglement, Proceedings of the thirty-fifth annual ACM symposium on Theory of computing, 2003.

[edit]