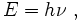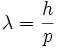From Wikipedia, the free encyclopedia

In physics, wave-particle duality holds that light and matter exhibit properties of both waves and of particles. It is a central concept of quantum mechanics. The idea is rooted in a debate over the nature of light and matter dating back to the 1600s, when competing theories of light were proposed by Christiaan Huygens and Isaac Newton. Through the work of Albert Einstein, Louis de Broglie and many others, it is now established that all objects have both wave and particle nature (though this phenomenon is only detectable on small scales, such as with atoms), and that quantum mechanics provides the over-arching theory resolving this apparent paradox.

Contents 1 History 2 Prehistory 2.1 Huygens and Newton; Earliest theories of light 2.2 Fresnel, Maxwell, and Young 3 Einstein and photons 4 De Broglie 5 Wave nature of large objects 6 Theoretical sketch and remarks on philosophical inquiry 7 Applications 8 See also 9 References

History

At the close of the 19th century, the case for atomic theory, that matter was made of particulate objects or atoms, was well established. Electricity, first thought to be a fluid, was understood to consist of particles called electrons, as demonstrated by J.J. Thomson by his research into the work of Rutherford, who had investigated using cathode rays that an electrical charge would actually travel across a vacuum from cathode to anode. In brief, it was understood that much of nature was made of particles. At the same time, waves were well understood, together with wave phenomena such as diffraction and interference. Light was believed to be a wave, as Thomas Young's double-slit experiment and effects such as Fraunhofer diffraction had clearly demonstrated the wave-like nature of light.

But as the 20th century turned, problems had emerged with this viewpoint. The photoelectric effect, as analyzed in 1905 by Albert Einstein, demonstrated that light also possessed particle-like properties. Later on, the diffraction of electrons would be predicted and experimentally confirmed, thus showing that electrons must have wave-like properties in addition to particle properties.

This confusion over particle versus wave properties was eventually resolved with the advent and establishment of quantum mechanics in the first half of the 20th century, which ultimately explained wave-particle duality. It provided a single unified theoretical framework for understanding that all matter can behave in both a wave-like and a particle-like fashion in the appropriate circumstances. Quantum mechanics holds that every particle in nature, be it a photon, electron or atom, is described by a solution to a differential equation, most typically, the Schroedinger equation. The solutions to this equation are known as wave functions, as they are inherently wave-like in their form. They can diffract and interfere, leading to the wave-like phenomena that are observed. Yet also, the wave functions are interpreted as describing the probability of finding a particle at a given point in space. Thus, if one is looking for a particle, one will find one, with a probability density given by the square of the magnitude of the wave function.

One does not observe the wave-like quality of everyday objects because the associated wavelengths of people-sized objects are exceedingly small. The wavelength is given essentially as the inverse of the size of the object, with the factor given by Planck's constant h, an extremely small number.

Prehistory

Huygens and Newton; Earliest theories of light

The earliest comprehensive theory of light was advanced by Christiaan Huygens, who proposed a wave theory of light, and in particular demonstrated how waves might interfere to form a wave-front, propagating in a straight line. However, the theory had difficulties in other matters, and was soon overshadowed by Isaac Newton's corpuscular theory of light. That is, Newton proposed that light consisted of small particles, with which he could easily explain the phenomenon of reflection. With considerably more difficulty, he could also explain refraction through a lens, and the splitting of sunlight into a rainbow by a prism.

Because of Newton's immense intellectual stature, his theory went essentially unchallenged for over a century, with Huygens' theories all but forgotten. With the discovery of diffraction in the early 19th century, the wave theory was revived, and so by the advent of the 20th century, a scientific debate over waves vs. particles had already been thriving for a very long time.

Fresnel, Maxwell, and Young

In the early 1800s, the double-slit experiments by Young and Fresnel provided evidence for Huygens' theories: these experiments showed that when light is sent through a grid, a characteristic interference pattern is observed, very similar to the pattern resulting from the interference of water waves; the wavelength of light can be computed from such patterns. Maxwell, during the late-1800s, explained light as the propagation of electromagnetic waves with the Maxwell equations. These equations were verified by experiment, and Huygens' view became widely accepted.

Einstein and photons

In 1905, Albert Einstein provided a remarkable explanation of the photoelectric effect, a hitherto troubling experiment which the wave theory of light seemed incapable of explaining. He did so by postulating the existence of photons, quanta of light energy with particulate qualities.

In the photoelectric effect, it was observed that shining a light on certain metals would lead to an electric current in a circuit. Presumably, the light was knocking electrons out of the metal, causing them to flow. However, it was also observed that while a dim blue light was enough to cause a current, even the strongest, brightest red light caused no current at all. According to wave theory, the strength or amplitude of a light wave was in proportion to its brightness: a bright light should have been plenty strong enough to create a large current. Yet, oddly, this was not so.

Einstein explained this conundrum by postulating that the electrons were knocked free of the metal by incident photons, with each photon carrying an amount of energy E that was related to the frequency, ν of the light by

where h is Planck's constant (6.626 x 10^-34 J seconds). Only photons of a high-enough frequency, (above a certain threshold value) could knock an electron free. For example blue light, but not red light, had sufficient energy to free an electron from the metal. More intense light above the threshold frequency could release more electrons, but no amount of light below the threshold frequency could release an electron.

Einstein was awarded the Nobel Prize in Physics in 1921 for his theory of the photoelectric effect.

De Broglie

In 1924, Louis-Victor de Broglie formulated the de Broglie hypothesis, claiming that all matter has a wave-like nature; he related wavelength, λ (lambda), and momentum, p:

This is a generalization of Einstein's equation above since the momentum of a photon is given by p = E / c where c is the speed of light in vacuum, and λ = c / ν.

De Broglie's formula was confirmed three years later for electrons (which have a rest-mass) with the observation of electron diffraction in two independent experiments. At the University of Aberdeen, George Paget Thomson passed a beam of electrons through a thin metal film and observed the predicted interference patterns. At Bell Labs Clinton Joseph Davisson and Lester Halbert Germer guided their beam through a crystalline grid.

De Broglie was awarded the Nobel Prize for Physics in 1929 for his hypothesis. Thomson and Davisson shared the Nobel Prize for Physics in 1937 for their experimental work.

Wave nature of large objects

Similar experiments have since been conducted with neutrons and protons. Among the most famous experiments are those of Estermann and Otto Stern in 1929. Authors of similar recent experiments with atoms and molecules claim that these larger particles also act like waves.

A dramatic series of experiments emphasizing the action of gravity in relation to wave-particle duality were conducted in the 1970's using the neutron interferometer. Neutrons, the stuff of atomic nuclei, provide much of the mass of a nucleus and thus of ordinary matter. Neutrons are fermions, and thus possess important quantity we associate with matter, namely "rigidness" (see Pauli repulsion of fermions). In the neutron interferometer, they act as quantum-mechanical waves directly subject to the forces of gravity. While not a surprise, as gravity was known to act on anything - even deflect light and act on photons (the Pound-Rebka falling photon experiment), the self-interference of the quantum mechanical wave of a massive fermion in a gravitational field had never been experimentally confirmed before.

In 1999, the diffraction of C₆₀ fullerenes by researchers from the University of Vienna was reported¹. Fullerenes are rather large and massive objects, having an atomic mass of about 720. The de Broglie wavelength is 2.5 picometers, whereas the diameter of the molecule is about 1 nanometer, i.e. about 400 times larger. As of 2005, this is the largest object for which quantum-mechanical wave-like properties have been directly observed in far-field diffraction. The experimenters have assumed the arguments of wave-particle duality and have assumed the validity of de Broglie's equation in their argument. In 2003 the Vienna group has meanwhile also demonstrated the wave-nature of tetraphenylporphyrin⁴ - a flat biodye with an extension of about 2 nm and a mass of 614 amu. For this demonstration the employed a near-field Talbot Lau interferometer ^2,3. In the same interferometer they also found interference fringes for C60F48, a fluorinated buckyball with a mass of about 1600 amu, composed of 108 atoms ⁴. Large molecules are already so complex that they give experimental access to some aspects of the quantum-classical interface, i.e. to certain decoherence mechanisms ^5,6.

Whether objects heavier than the Planck mass (about the weight of a large bacterium) have a de Broglie wavelength is theoretically unclear and experimentally unreachable. The wavelength would be smaller than the Planck length, a scale at which current theories of physics may break down or need to be replaced by more general ones.

Theoretical sketch and remarks on philosophical inquiry

The wave-particle paradox is resolved in the theoretical framework of quantum mechanics. This framework is deep and complex and therefore impossible to adequately summarize in brief.

Every particle in nature, be it a photon, electron, atom, et cetera, can be described in terms of the solution to a differential equation, most typically the Schroedinger equation, but also through the Dirac Equation. These solutions are mathematical functions called wave functions, as they contain oscillatory mathematical components and are hence inherently wave-like in nature. Wave functions can diffract, interfere with one another or themselves, and otherwise accurately predict observed wave-like phenomena such as is described in the double-slit experiment.

Wave functions are often interpreted as describing the probability of finding their corresponding particle at a given point in space at a given time. For example, upon setting up an experiment involving a moving particle, one can 'look' for that particle to arrive at some particular location using a detection apparatus set up at that location. While quantum behavior follows well-defined deterministic equations (such as the wave function), the solutions to these equations are probabilistic. The probability of the detector detecting the particle is calculated by taking the integral of the product of the wave function and its complex conjugate. While the wave function can be thought of as smeared out in space, in practice the detector will always either *see* or *not see* the entire particle in question; it will never see a fractional piece of the particle, like two-thirds of an electron. Hence the strange duality: The particle propagates in space in a distributed, probabilistic wavelike fashion but arrives at a detector as a localized, complete corpuscle. This paradoxical conceptual framework has some explanations in the forms of the Copenhagen interpretation, Path Integral Formulation, or the Many Worlds Interpretation. It is important to realize that all of these interpretations are equivalent and result in the same predictions even though they offer widely different philosophical interpretations.

While quantum mechanics makes astoundingly accurate predictions about the outcomes of such experiments, its philosophical meaning is still sought after and debated. This debate has evolved as a broadening of the original struggles to comprehend wave-particle duality. What does it mean for a proton, to behave both as a particle and as a wave? How can an antimatter electron be mathematically equivalent to a regular electron moving backwards in time under certain circumstances, and what implications does this have for our experience of time as one-directional? How can a particle seemingly teleport through a barrier while soccer balls regularly fail to pass through cement walls? The implications of these facets of quantum mechanics continue to puzzle many who delve into the subject. (The discussion currently can be investigated further under headings of local realism and quantum measurement.)

Some physicists intimately associated with the historical struggle to arrive at the rules of quantum mechanics have viewed these philosophical debates on wave-particle duality and related matters as attempts to impose human experience on the quantum (microscopic) world. Since by its nature this world is completely non-intuitive, quantum theory (they would assert) must be learned on its own terms independent of experience-based human intuition. The scientific merit of searching too deeply for a 'meaning' to quantum mechanics is thereby suspect; (Bell's theorem and experiments it inspires provide a good example of such testing of the foundations of quantum mechanics.) From a physics viewpoint, the inability of a new quantum philosophy to satisfy the testability criterion or alternatively the inability to find a flaw in the predictive power of the existing theory reduces to a null proposition, perhaps even risking degeneration into pseudoscience.

Applications

Wave-particle duality is exploited in electron microscopy, where the small wavelengths associated with the electron can be used to view objects much smaller than what is visible using visible light.

See also

• This entry is still rather rudimentary. It would be very desirable to add a information on the huge amount of literature on atomic beam interferometry, Bose Einstein Condensation, decoherence experiments as well as interesting papers on diffraction of cold molecules and several recent electron interference studies.
• Afshar experiment
• Arago spot
• Hanbury-Brown and Twiss effect
• Scattering theory

References

• Note 1: Arndt, Markus, O. Nairz, J. Voss-Andreae, C. Keller, G. van der Zouw, A. Zeilinger (14 October 1999). "Wave-particle duality of C60". Nature 401: 680-682.
• Note 2: Clauser, John F., S. Li (1994). "Talbot von Lau interefometry with cold slow potassium atoms.". Phys. Rev. A 49: R2213-17.
• Note 3: Brezger, Björn, Lucia Hackermüller, Stefan Uttenthaler, Julia Petschinka, Markus Arndt and Anton Zeilinger (2002). "Matter-wave interferometer for large molecules". Phys. Rev. Lett. 88: 100404.
• Note 4: Hackermüller, Lucia, Stefan Uttenthaler, Klaus Hornberger, Elisabeth Reiger, Björn Brezger, Anton Zeilinger and Markus Arndt (2003). "The wave nature of biomolecules and fluorofullerenes". Phys. Rev. Lett. 401: 680-682.
• Note 5: Hornberger, Klaus, Stefan Uttenthaler,Björn Brezger, Lucia Hackermüller, Markus Arndt and Anton Zeilinger (2003). "Observation of Collisional Decoherence in Interferometry". Phys. Rev. Lett. 90: 160401.
• Note 6: Hackermüller, Lucia, Klaus Hornberger, Björn Brezger, Anton Zeilinger and Markus Arndt (2004). "Decoherence of matter waves by thermal emission of radiation". Nature 427: 711-714.
• R. Nave. Wave-Particle Duality. (Web page) HyperPhysics. Georgia State University, Department of Physics and Astronomy. URL accessed on December 12, 2005.
• Markus Arndt (2006). Interferometry and decoherence experiments with large molecules. (Web page) University of Vienna. URL accessed on May 6, 2006.