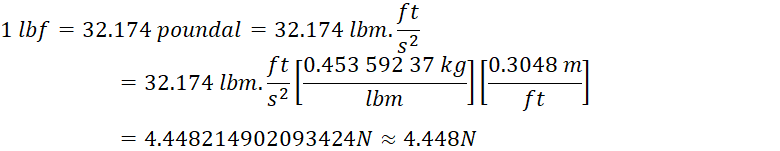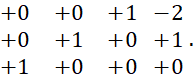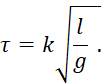1. Coordinate geometry. Cartesian, cylindrical, and spherical coordinate systems. Quadratic equations. Numerical analysis—nonlinear equations and systems of linear equations. Simple differential equations.

2. Vector algebra—vectors, magnitude of a vector, addition and subtraction of vectors, components of a vector, triangle law (the magnitude of the sum of two vectors is less than or equal to the sum of the magnitudes), multiplication of a vector by a scalar, scalar (dot) and vector (cross) products.

3. Differentiation and integration of scalar and vector functions of a single variable.

4. Units and dimensions for mechanical systems. SI system—second, meter, kilogram (will not need ampere, degrees Kelvin, mole, and candela). Transformation of units from one system to another. Simple dimensional analysis may be introduced but will not be assumed.

Newton’s laws of motion

The original form, translated from Latin

1. Every body continues in its state of rest, or of uniform motion in a straight line, unless it is compelled to change that state by forces impressed upon it.

2. The change of motion of an object is proportional to the force impressed; and is made in the direction of the straight line in which the force is impressed.

3. To every action, there is always opposed an equal reaction; or, the mutual actions of two bodies upon each other are always equal, and directed to contrary parts.

Preliminaries

1. Space is Euclidean and there is a reference frame in which the first law, below, is true.

2. Time is homogeneous, which means that that there are elementary devices (clocks), such that the second law, below, is true.

3. The world is made of point particles that have constant scalar mass and variable vector position (which may be constant in some cases). If is an index that labels the particles, the masses are , and positions , which are functions of time, (scalars are italicized and vectors are bold). If there is just one particle, the index may be omitted.

4. Force is a vector interaction between particles and sums vectorially. The sum of the forces on particle is written, .

5. The velocity, , and acceleration, , of a particle are the first and second derivatives of position with respect to time.

6. The momentum of a particle, , is the mass times the velocity.

In modern form

1. The momentum of a particle is constant if and only if the external forces on it sum to zero.

2. The rate of change of momentum of a particle is equal to the sum of the forces on it.

3. The mutual forces of two particles on one another are equal in magnitude, opposite in direction, and lie on the straight line through the particles.

Comments

1. Newton’s original statement of the second law was that “change in motion is proportional to the motive force impressed”. By “change in motion” he meant “rate of change of momentum”, by “motive force impressed” he meant “the sum of the applied or external forces”. Given units for time, length, and mass, the units for force can always be chosen so that the constant of proportionality is 1. We will do this and so—

Some older texts define force independently, in which case the constant of proportionality is not 1, and such texts often write

We will not use this form of Newton’s second law. There is another form of the law that we will not use either. It is a form in which weight is used instead of mass. With W as weight, W=mg, therefore Newton’s second law is—

2. A frame of reference for which the first law holds is called ‘inertial’. If a second frame moves at constant or zero velocity and does not rotate relative to an inertial frame, the second frame is also inertial. If the velocity of the second frame is not constant or if it rotates, it is not inertial, and the first and second laws must be modified.

3. The first law is a special case of the second law. Though it highlights the existence of inertial frames, so does the second law. Perhaps Newton included it for it was emphasized by Galileo as the law of inertia.

4. Such modifications may be introduced via ‘inertial forces’, e.g., the centrifugal force, which are of significant historical interest. But inertial forces are not interactions between particles and because their use can be unnecessarily confusing, we will talk of them mainly in passing.

5. The importance of the second law is that (i) given the forces, it determines the motion or (ii) given the motion, it determines the force.

6. Although the laws are stated for particles, the extension for bodies is simple. It will be derived later. For now, we note that the second law generalizes to bodies with the vector as the position of the body’s center of mass (or, if the body is small compared to the scale of motion, the position of a conveniently chosen point in the body).

7. The importance of the third law is that (i) without it the important laws of conservation of energy, momentum, and angular momentum would not hold (ii) the second law for particles would not generalize to bodies—it generalizes because the internal forces cancel out (iii) it is critical to force analysis and so to problem solving in physics and engineering. In doing force analyses, it is important to remember that if the action is the force of a first body on a second, the reaction is the force of the second on the first (and so, since action and reaction are on different bodies, they do not cancel in summing the forces on any of the bodies).

About forces

Gravity

Newton’s law of gravitation is that the force between any two particles is an attractive force that is proportional to the masses and inversely proportional to the square of the distance between the particles. This can be written—

where is the force of particle on particle , is the universal gravitation constant, the distance between the particles, and the unit vector from particle to particle . The minus sign on the right means that gravity is always attractive.

The shell theorem of Newton

Newton proved that a thin uniform shell has a gravitational field that (i) inside the shell is zero (ii) outside the shell is as if the mass of the shell were concentrated at its center. It follows that for a uniform sphere (i) inside the sphere, the field is proportional to distance from the center (not too hard to show) (ii) outside sphere, the field is as if its mass is at its center.

Since interplanetary distances are large, it is intuitive that to concentrate mass at the center of the sun and the planets is a good approximation. The shell theorem shows this to be precise. If the bodies are not perfectly spherical, concentration of the mass at some point in (usually) the interior, is a good approximation.

Gravity on the surface of the earth

For heights small compared to the radius of the earth, gravity is approximately constant. While gravity at the surface of the earth varies, a standard value is—

Electromagnetism

Beside gravity, most forces at or above the atomic level are electromagnetic in origin. These include forces of compression in a substance and the reaction between at the surface between two substances. Electromagnetism is beyond the scope of introductory mechanics. The special case of electrostatic force—the force between to stationary point charges follows a law similar to gravity—

where is charge, the ratio of circumference to diameter of a circle, and the ‘permittivity of free space’. The absence of a minus sign means that two like charges repel and unlike charges attract.

Spring force

Springs are common in engineering and elementary physics. Though the molecular basis is complex, spring forces can be written simply—

Where is the force is the ‘spring constant’ and extension of the spring, which is positive in elongation and negative in compression (the minus sign means that the force tends to restore the spring to its original length).

Many actual situations are approximated by the ‘spring equation’ above in which force is proportional to extension. A slightly more complex equation covers more cases—

The term represents ‘nonlinear effects’ and in which is the time derivative of , represents friction (the minus sign means that viscous friction opposes motion).

Contact forces—friction and normal reaction

The interaction force at a surface between two solids is conveniently decomposed into two components—a normal reaction and friction force , which are, respectively, normal and parallel to the tangent at the point of contact.

The law of ‘dry static friction’, written, , where is the ‘coefficient of static friction’, gives the value of below which relative motion of the surfaces does not occur and at or greater than which motion occurs. That depends only on the materials and is independent of is an approximation. The word ‘dry’ indicates that the surface is not lubricated (for well lubricated surfaces, motion will occur for any non-zero , which, as an approximation, will be proportional to the relative tangential velocity of the surfaces). Once motion is occurring, the force of friction is given by where is the ‘coefficient of kinetic friction’, which is somewhat less than .

Units and dimensions

Units

It is usual in mathematics for symbol to designate a ‘pure quantity’—a number or vector and so on—without an associated unit. Thus—

However, a number cannot specify a physical quantity for we would need to know “10 of what”. The ‘what’ is usually a ‘unit’. Thus, a length, distance, or position can be specified—

which specifies a length or distance of .

Fundamental units

In a situation where distance is the only variable of interest we need just one unit—a unit of length. If we were interested in area, we do not need to introduce another unit for the units of area are expressible in terms of length, e.g., , is an area of 10 square metres. Thus, for geometry, we need just one ‘fundamental’ unit.

To describe motion, we specify position as a function of time. We therefore need two units—time and distance. Examples—

The dot between m and s above is optional but will avoid confusion be necessary when the unit symbols are not single letters. Also note that we could also write , but not , which would be confusing.

In dynamics, a third fundamental unit is needed. Mass is most common, and a mass of ten kilograms would be written,

For dynamical quantities and equations, three fundamental units are sufficient.

Units for force can be derived from Newton’s second law—thus a force to accelerate at , is—

The ‘’ could be confusing but with familiarity it will not be. However, there are situations where the dot between unit symbols is needed.

Which suggests defining a unit of force—

In terms of which the force , above is .

We defined the unit of force in terms of units of mass, length, and time. We could (i) also introduce an independently defined unit of force, but this is redundant and results in an unnecessary complication (ii) introduce an independently defined unit of force rather than mass, but it is easier to specify a standard mass than a standard force—so practice in science and this text, will use mass, length, and time as fundamental.

Independently defined units of force

However, since independently defined units of force are often used, especially in older texts and practice, we will discuss them, even though their use in this text is minimal.

The kilogram force, or is the weight of a kilogram mass, at a place where the acceleration due to gravity is the standard value of .

Dimensions

The concept of a dimension is that it refers to the kind of units of a physical quantity, but not its magnitude. If is a physical quantity, is read the ‘’. For dimensions of base unit quantities their dimension will be a single letter, e.g., for length. This is because they are generally (but not always independent) quantities. Thus, the dimensions for time, length, and mass are written—

The dimensions of other quantities in dynamics can be derived. Thus, since velocity, , is distance over time,

and, similarly, for acceleration, momentum, force, and energy , which are also in the table of derived units below.

Base units

We have decided on time, length, and mass as fundamental in dynamics, which is consistent with the International System or SI, in which the base units are the second, metre, and kilogram as base units. For completeness here is a system of base SI units for physics—

Unit name	Unit symbol	Dimension symbol	Quantity name
Second	s	T	time
Metre	m	L	length
Kilogram	kg	M	mass
Ampere	A	I	electric current
Kelvin	K	Θ	thermodynamic temperature
Mole	mol	N	amount of substance
Candela	cd	J	luminous intensity

Derived units

Physical quantity	Name	Symbol	Dimension	In terms of base units
Angle	Radian	rad
Solid angle	Steradian	sr
Acceleration		a
Force, F	Newton	N
Momentum, p		p
Energy, E	Joule	J

Dimensions

For a distance , the common aspect or dimension is length, , so writing the dimension of as —

Similarly, for

In dynamics, time and length are independently defined ‘dimensions’. A third independent unit is either force or mass. From Newton’s second law, given either force or mass, the unit for the other follows.

The basic units for dynamics in the SI system are the second, meter, and kilogram. The table below shows independent units for dynamics and other areas of physics.

Physical quantity	Name	Symbol	In terms of base units
Time	Second	s
Length	Metre	m
Mass	Kilogram	kg
Angle	Radian	rad
Solid angle	Steradian	sr
Force	Newton	N
Momentum
Energy	Joule	J

Unit conversions

English Engineering units (not used in England or in this course) foot-pound-second—

(definition), therefore

Derived units can be force or mass (needlessly confusing, but in an attempt at some consistency)—

(definition)

(definition), therefore

, or

(definition), therefore

, or

Unit conversion—an example

The constant of proportionality in Newton’s second law

Though we will not use the constant introduced earlier, it is useful to consider it briefly. If a force of is applied to a , the acceleration is . Therefore

Dimensional analysis

Dimensional analysis is based on the fact that added and equal physical quantities must have the same dimensions (units); however, different physical quantities may be multiplied and divided—but this does not change the point about equal physical quantities since both sides of equations must be multiplied by the same factor.

Simple dimensional analysis example

To what height, , does a body thrown up with velocity , ascend?

We will write dimensions of a physical object as . Then,

Assume

Then, taking dimensions, with ,

We get

Which results in

Or,

Little physics goes into dimensional analysis. It does not give us the value of the constant k, which we know from simple physics, is .

The Buckingham pi theorem

Given a physical equation which has variables , , … , , which contain primary dimensions … , the equation may be written in terms of , dimensionless variables or groups, , , , … , where is the rank and the nullity of the dimensional matrix or , defined by writing the as a product of powers of , and then

Thus

becomes

Example for the pi theorem

Let’s look at the height example. There are three parameters , , and , and two primary dimensions, , [, and ; therefore, the matrix is—

Which has rank 2 and therefore there is one dimensionless parameter,

and a solution of the form,

goes through as before (we may take without losing generality).

A second example for the pi theorem—frequency of a pendulum

The pendulum has mass and length . We will find its period . The primary dimensions are , , and . The dimensions of the four parameters are , , , and ; the dimensional matrix is

The rank is 3 and there is one dimensionless parameter

On solving we get, with a constant of proportionality—