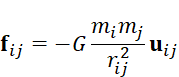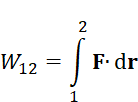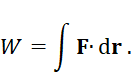Classical Mechanics

This work is part of a series

Contents

In-process plan

Introduction

What classical mechanics is

The continuing importance of classical mechanics

The aim of the work

The aim of the series

Newton’s formulation in modern terms

Elementary notions

Notation and definitions

In-process plan

Similar articles are planned for a range of disciplines in connection with the aims of the way of being and particularly with the essay, a system of human knowledge. The articles are not intended to be only qualitative but to bring myself up to the point where I can understand and perhaps participate in further study (research). Naturally, that aim might be achieved in only a few areas.

1. Arranging the contents

2. Improve formatting of the table of contents, the headings, the text, the formulas, and the comments.

3. Distinguish essentials, commentary, and philosophy

4. Place thermodynamics appropriately

5. Develop the following topics:

Analytical, variational, and geometric (manifold) formulations.
Why the idea of inertial forces will be noted but not used.
Fields.
Applications and problems.
Thermodynamics with and without statistical mechanics.

Introduction

What classical mechanics is

In physics, the term ‘classical’ may refer to a range of theories defined by the following extremes (i) all but quantum physics (ii) only those theories that are non-quantum and Galilean invariant. Regardless of use, classical mechanics is classical physics.

Classical mechanics is the mechanics of Isaac Newton and its various formulations which include (i) Newton’s original formulation whether written in his terms or in vector or tensor form—with extensions to momentum, angular momentum, and energy formulations (ii) the analytical formulations including those of Lagrange and Hamilton (iii) modern geometric formulations beginning with Poincare and employing analysis on manifolds (iv) a range of exact, approximate analytical, and numerical solution techniques and applications.

The continuing importance of classical mechanics

Though classical mechanics, which began with Isaac Newton, is not a modern theory of matter and motion, it is important to engineering, mathematics, foundations of quantum and relativistic physics, philosophy (Newton was also a philosopher), the idea of a scientific paradigm, the development of science-based technology, and the history of science. It continues to be of mathematical interest and to have new applications, e.g., in space dynamics, where its classical nature still is an excellent approximation. Finally, in learning modern physics, classical physics is an essential preliminary.

The development begins with Newton’s formulation. I plan to add a range of (i) analytical formulations, beginning with the Lagrangian and variational and (ii) classical and modern solution approaches and applications.

The aim of the work

The article is intended to be an outline of classical mechanics—foundations, elementary notions, elementary through analytical formulations, axioms or laws, results or theorems, and other applications.

It is intended to be reasonably comprehensive in topics but not in coverage. Generally, proofs will be omitted, and explanation and historical material kept to a minimum.

The aim of the series

This work is part of a series of works on topics that (i) interest and challenge me and (ii) might be useful to me in the formation of a comprehensive world view.

The first aim of the series is personal. It is an element in the development of my work on the way of being.

While it was not my original intent to publish these works, I will be pleased if they are found useful.

Newton’s formulation in modern terms

‘Modern terms’ means the vector formulation typical to textbooks in the early twenty-first century (scalar, matrix, and tensor formulations may also be used). Familiarity with vector algebra and calculus is presumed. In formulas bold letters are vectors, other letters are scalars, which are usually italicized.

The approach to dynamics on (symplectic) manifolds will be developed later.

See web and local sources (the local source is available only on a private network).

Elementary notions

This is to be revised—we begin with primitives, axioms, theorems, and pictures (gif’s or jpg’s)

The elementary notions are

(i) Euclidean space and position in space,

(ii) A uniform time continuum and location in time,

(iii) mass,

(iv) a system of point particles numbered

of unchanging masses ,

with position vectors , relative to the origin of the frame, which are functions of time, ,

and thus

(v) causes or fundamental correlates of motion and structure in systems—a system of particle-particle interactions or forces (vectors)

, the force of particle on particle ,

which system has space and time symmetry (from time symmetry it is unnecessary to have stated that the time continuum is uniform).

On the concept of accelerative forces. Forces are interactions. For non-inertial frames, the acceleration is seen to be the acceleration relative to the frame plus terms that arise due to motion relative to an inertial frame. Thus, for non-inertial frames, the Newton’s second law, below, will be modified to include these terms—in a non-inertial frame the law is no longer the simple form

The simple form may be regained by defining ‘minus mass times relative acceleration terms’ as an accelerative force (also called inertial force and reverse effective force). Such forces include centrifugal and Coriolis forces which have an intuitive appeal and some explanatory and formal use. However, in the Newtonian scheme, forces are interactions and the accelerative forces, therefore, in this scheme, are not true forces. It has been said that the equivalence of gravitational force and acceleration in general relativity shows that inertial forces are true forces; however, beside the fact that relativity is another scheme, equivalence is not identity and, further, the equivalence is only local and, what is more, is not true for other fundamental forces. Inertial forces are an unnecessary concept (their formal uses being historical but unnecessary) and can be confusing in computational situations, where a direct approach without inertial forces is straightforward. It is therefore my preference to not use inertial forces for formal or computational purposes.

Corollary to the elementary notions. If the system is spatially homogeneous and symmetric, a particle-particle interaction will not be a function of orientation and will lie along the line joining the particles. If it is homogeneous with regard to time, the interactions will not be functions of time. Therefore, if symmetric in space and time, the interactions will be functions only of distance between the particles and lie on the line joining the particles.

The Newtonian framework does not require the dimension of space to be 3. Since we find our physical space to have 3 dimensions, 3 is the usual number (strictly that real space is of dimension 3 is hypothetical, and that it is Euclidean is hypothetical and approximate. In the general case of a collection of particles, extension to any number of dimensions is easy. However, kinematics and rigid body motion in higher dimensions is more complex that in the lower dimensional cases. Two dimensional considerations are particularly simple.

That time is a continuum shall mean that it is a real number continuum—which, too, is hypothetical for, while the real number system lends itself to the application of mathematical analysis, perhaps other systems, e.g., the rationals or the surreals are more realistic, according to the application. Perhaps we ought to inquire, why over and above mathematical convenience, any particular number should be chosen. Ought it be determined by physical or empirical considerations? There do not seem to be any physical considerations from classical physics, except perhaps from limitations of measurement. But Newtonian physics offers no insight into intrinsic limits. On the other hand, optics does suggest limits—measurement cannot be finer than the wavelength of the region of the electromagnetic spectrum used for measurement. Considerations of atomism suggest that mechanical measurement be limited by atomic dimensions. But are there intrinsic limits? If the cosmos is a quantum state, then the proper system of representation might be, not an arbitrarily chosen mathematical system, but the characteristic quantum states (‘eigenstates’).

In the Newtonian framework two particle, spatially symmetric, time independent interactions are set up as fundamental: interactions that are functions of time, which depend on orientation, or are other than two particle interactions, are not fundamental, and are the result of changing distributions of matter. This does not imply that two particle interactions must be fundamental; in fact, gravitation might be a function of the distribution of matter in the entire cosmos; however, while such a function might be derived in a general relativistic framework, it does not seem that this could be done in the Newtonian framework. The Newtonian scheme of forces does not include the electromagnetic.

Notation and definitions

The position , of a particle relative to a Euclidean frame is—may be represented as—a vector (noted earlier).

The velocity , and acceleration , of particle i are the first and second order time derivatives of position, and , respectively.

The (linear) momentum is .

The angular momentum in the frame is the vector cross product, .

Corollary. If the center of mass (cm) of a system of particles of total mass is defined by

the total momentum

and the angular momentum

i.e., angular momentum of the entire mass at the cm plus angular momentum of the particles relative to the cm, where the stars are the objects, relative to the center of mass.

The force or net force on a particle is the sum of the forces of all particles on it.

The moment

, of a force , about a point , is ,

where a position vector for any point on the line of action of , relative to ,

(the moment of a system of forces about is the sum of the moments about ).

The moment of a system of forces about a point is given by

where

is the sum of the forces, and

is the position vector for relative to , which equals .

If the sum of a system of forces is , their moment is the same about all points.

A couple is a pair of equal and opposite but not necessarily collinear forces. Given a couple, its moment is the moment of the two forces, which, since the sum of the two forces is zero, is independent of the point about which the moments are taken. The same symbol may be used for a couple and its moment.

Given a system of forces and any point , there is a single force through or at and couple that have the same net force and moment as the system. is the sum of the forces, and is the sum of the moments about . If is , then is independent of .

Axioms (laws)

1. The first law. There is a frame, called an inertial frame, in which, if the net force on a particle is zero, its momentum and velocity are constant.

Corollary. If the first law holds in a frame, it holds in any frame moving at constant velocity relative to the given frame.

The forces are not, as Aristotle held, fundamentally causes of momentum, for if they were, a particle with zero net force would have zero velocity—it would be at rest.

2. The second law. For any frame in which the first law holds, i.e., for inertial frames, the rate of change of momentum of a particle is equal to the net force on the particle.

That is, if the net force on a particle of mass is , acceleration is given by . For systems, we write .

Queries. Why is the force equal to the time derivative of momentum of first order? That is, why does the force equation involve the second time derivative of position? Why not, as Aristotle thought, the first order time derivative? What would the world be like if Aristotle were right? Why are time derivatives of order higher than 2 not present?

The first law is a special case of the second. Possible reasons for Newton’s statement of it are (i) it was an insight due to Galileo and is known as Galileo’s law of inertia (ii) it stands in opposition to the classical idea of Aristotle that uniform motion requires a force to sustain it (iii) it is of special importance in making clear that there are inertial frames.

No perfectly inertial frames are known. For motion near the surface of earth, earth itself is often good enough. A better frame is one fixed in the center of mass of the solar system, called the barycenter (of the solar system) and which varies in position relative to the sun but lies within the sun or near its surface. However, this too is imperfect. It was thought that there is a perfect inertial frame defined by the ‘fixed stars’. However, at those scales, Newtonian mechanics breaks down—giving way to general relativity, which is an improvement over Newtonian mechanics. This comment is continued below, as a comment following the discussion of universal gravitation.

3. The third law. The mutual forces for any two particles are equal, opposite, and lie on the line joining the particles—that is,

It follows that the form of must be

, , or ,
i.e., the product, a scalar , and the unit vector from to .

is attractive or repulsive as it is negative or positive, respectively. If the earlier symmetry arguments are sustained, is a function only of the magnitude .

Corollary. (1) The self-force of a particle, is , i.e., particles do not exert forces on themselves. (2) In an inertial frame, the rate of change of momentum of a system of particle is the net force on it. (3) The rate of change of angular momentum of a system is the sum of the moments of the external forces (for an inertial frame).

By the third law, the action of one particle on another and the reaction of the second on the first are equal, opposite, and collinear. This formulation is Newton’s and forestalls the elementary confusion as to how, if action and reaction are equal and opposite, there can be motion at all. That action and reaction are equal and opposite, results in conservation of momentum (we may consider self-force to be non-zero, but it would result in an unstable world in which particles without any net—external—force would accelerate in inertial frames). That action and reaction are equal, opposite, does not result in conservation of angular momentum, but it does follow if the forces are also collinear. The third law holds for electrostatics and magnetostatics but does not hold for electromagnetism. However, electromagnetic fields can be assigned momentum and angular momentum, in which case the third law holds if field interactions are also considered, and then linear and angular momentum are conserved.

4. Universal gravitation. Every particle attracts every other, with a force called ‘gravitation’, which is proportional to the products of their masses, and inversely proportional to the square of the distance between the particles. The constant of proportionality G is the same for all particle pairs and is called the universal gravitation constant. The form of the law is

Query. Why does gravitational attraction follow an inverse square law? What is the significance of this law?

Corollaries. (1) Given a massive particle , and other particles , which impart no motion to m (because it is so massive), the accelerations of all the (other) particles varies inversely as the square of their distance from m—that is, the accelerations do not depend on mass. (2) Given a uniform shell of mass m, its gravitational field (i) outside the shell is that of a point of mass m placed at the center and (ii) zero inside the shell. (3) Given a uniform massive sphere, the acceleration due to its gravity is the same everywhere at a given distance from its center. (4) It is an experimental fact that the acceleration due to gravity near the surface of the earth of all objects is about 9.82 meters per second per second and is approximately the same everywhere and for elevations not too large. The variation at the surface of the earth is due to the earth not being perfectly spherical and uniform, and the rotation of the earth. The smallness of variation with height obtains only at elevations small compared to the radius of the earth. (5) The attraction and path motion of the centers of mass of two uniform spheres is as if the entire masses were at the centers of the spheres.

The attraction and path motion of arbitrary bodies is similar to that of two uniform spheres, with small corrections provided the spheres are not close and the times not too long. The mathematics of the corrections is complex.

Theorem. The center of mass of a body rotating about a fixed center with inverse square force describes an ellipse. For two bodies with inverse square attraction, the motion is reducible to the problem of a single body.

For three and more bodies, the problem is far more complex and only a limited number of closed form solutions are known.

On the source of universal gravitation and the apparent identity of inertial and gravitational mass. These source of these two features of universality and identity is a seeming mystery, contemplated by Newton himself, by Ernst Mach, and Einstein. Mach suggested that the source of gravitation is an aggregate effect of all the matter in the universe, and this would make the for the two features to be reasonable and to have a common source (this is further discussed in philosophical commentary on the Newtonian scheme).

Momentum and impulse

We saw that the rate of change of momentum of a particle is equal to the net force on it.

For a system of particles, the rate of change of momentum is the sum of the forces on the particles, which, from Newton’s third law, is the sum of the external forces—i.e., simply, the external force on the system.

For a system of particles, then,

where

is the external force on .

If the external force on a system vanishes, its momentum is conserved—i.e., the momentum is unchanging.

For the momentum and conservation of momentum laws to hold, it is not necessary for action and reaction pairs to be collinear.

For a given time interval, if the impulse of a force is defined as its integral with respect to time, then the change of momentum of a system is equal to the impulse of the external forces (i.e., the sum of the impulses of the external forces).

Angular momentum

For a system of particles, the rate of change of angular momentum is the sum of the moments of the forces on the particles, which, from Newton’s third law, is the sum of the moments of the external forces—i.e., simply, the external moment on the system. This is of course for an inertial frame and the moments and angular momenta are relative to the origin of the frame.

Recall from notation and definitions, that we can write that the momentum

and the angular momentum

If the external moment on a system vanishes, its angular momentum is conserved—i.e., the angular momentum is unchanging.

For the angular momentum and conservation of angular momentum laws to hold, it is necessary for action and reaction pairs to be collinear.

Energy

Though internal forces do not affect changes in momentum and angular momentum, they do affect energy.

Define the work done by a force as the integral over a path of the force with respect to position—

Consider the system of particles with positions . There are internal forces and external forces .

A force is called conservative if it is derivable from a potential such that , where is the ‘gradient’ operator. If a force being is conservative the work done on any path depends only on the end points—and that the work for a closed path is zero. If a force is not conservative, i.e., if it is non-conservative, the work done generally depends on the path and does not vanish for a closed path. The significance of the term ‘conservative’, as will be seen, is that if all forces are conservative, total energy is conserved.

Let any force be written

where conservative and is unspecified but may have a non-conservative part.

If the force equations are integrated with respect to position, the following is obtained—

Define the kinetic energy of a particle as

from which the total kinetic energy of a system, the sum of the individual kinetic energies is

= = .

Define the potential energy as

Note that some authors write a factor before the term , above to emphasize that the pair, and , are just one potential. Here, the summation sign is intended as counting the pair as one.

Define the and total energy,

Then, integrating the force equations with respect to position, from position 1 to position 2, and with as the contribution of non-conservative forces from initial position 1 to final position 2,

Note that the internal forces, conservative and other, may contribute to the work, even though they balance; this is the general case and occurs because though they balance, their displacements may be different.

If all forces are conservative and represented by a potential, then the total energy of the system is conserved.

For conservative systems,

Comments on non-conservative or dissipative forces. On ordinary time and space scales all forces are regarded as conservative. However, if we look only at macroscopic mechanical energy, kinetic and potential, we find that it may be converted into ‘internal’ energy, i.e., molecular kinetic and potential energy. The transformation is called ‘dissipative’ and examples are friction and viscous forces. Thus, while there may be loss of macroscopic energy, total energy is conserved. Often the dissipation is small enough that the macroscopic process may be regarded as conservative. In other situations, dissipation is significant.

Intuitively, because molecular motion is coherent in macroscopic processes but lacks coherence for internal molecular processes, dissipation is always a conversion from macroscopic to molecular. The reverse is not mechanically impossible but intuitively unlikely. That these heuristic arguments are true is borne out by experiment and is also a consequence of the second law of thermodynamics, which is founded in molecular statistics and whose probability exception is so low on ordinary scales, that the law is essentially deterministic.

More on the Newtonian framework

The source or origin of the framework is not clear. However, (i) in a relatively stable cosmos with coherent behavior, there must be some form and some coherent relation between form and change (the paradigm of mechanics is a relation between form, relation among form, and change, but such relation is a part of form) and, further, ‘force’ is a name for relations between form and change (ii) if there is a tumultuous background universe, with beings randomly phasing into and out of being, and if the background is sufficiently rich with possibility, then near stable and therefore more than transient cosmoses will emerge, with the stability being due to near symmetry (iii) and the elementary components of such cosmoses may be capable of higher forms of being.

As best he could, Newton motivated and roughly derived his system from observation, guided by reason. However, there was no strict implication from observation, and it is not clear that the system, especially gravitation, are fundamental over and above being predictive and correlative—and Newton knew and wrote of this in his famous work on mechanics.

Possible extensions

Particles with angular momentum, elementary couples, higher order moments.

More on forces

Though the forces considered here are not fundamental, they are of practical importance.

The electrostatic and magnetostatic forces are aspects of a fundamental force, the electromagnetic force. This force, however, does not fit into the Newtonian framework.

In addition to gravity, the following forces are often encountered in practical applications.

1. Dry solid friction. The behavior and theory are complex. However, unlike gravity, which can be assigned a ‘potential energy’, such that for gravitational systems total (potential + kinetic) energy is conserved, friction does not seem to be conservative. But forces are conservative at the atomic level, and the macro or mechanical level non conservative behavior of friction is due to conversion of mechanical (potential + kinetic) energy into internal (molecular) energy (these comments can be made precise). The mechanism of dry friction is micro interactions at surfaces. For many purposes, the force of dry friction is proportional to the normal force, and the constant of proportionality is called the coefficient of friction. This constant depends on the surfaces and upon whether motion begins (static coefficient) or is maintained (kinetic).

2. Fluid film friction. Fluid films between two surfaces, reduces friction force, heat, and wear. The subject is complex. Integrity of the film is maintained hydrodynamically or with external pressure. In the simple case where the film does not break down, and the surfaces are effectively rigid, the friction force is proportional to velocity.

3. Object moving through a fluid. At low speeds, the friction force is (approximately) proportional to speed; at higher speeds it is proportional to the square of the speed. The transition between the two phases is determined the value of the “Reynold’s number” which is a function of viscosity, speed, size of the object, and fluid density.

4. Spring force. In many mechanical and other systems, the restoring force about a point of static equilibrium is proportional to the displacement. This is a simple but useful model. If there is only one displacement parameter, the motion in absence of friction and other external forces is sinusoidal and named ‘simple harmonic motion’. This observation is a point of entry into the topics of forced vibrations, vibrations with friction, and vibrations and waves for multi-degree of freedom and continuous systems, and vibrations and waves for nonlinear systems.

5. Linear vibrations about an equilibrium point. This generalizes the previous point. If the forces vary sufficiently smoothly with position and are not functions of time, then, for sufficiently small displacements from equilibrium, the equations of motion on the position coordinates are a system of second order linear differential equations with constant coefficients. If the equilibrium is stable, then, without friction, the motion is a superposition of simple harmonic motions. While nonlinear systems and non-autonomous (time dependent) coefficients have significant application, the case just considered has wide practical application. It informs us of the frequencies of vibration and, further, if there are exciting forces, it can be shown that if the exciting force and the vibratory frequencies are the same, there will be resonance, which may, in some cases, be destructive, and, in other cases, be useful.

6. Electrostatic and magnetostatic forces. At this point we only mention such forces and their significant generalization—electromagnetism.

7. Other forces. While the fundamental forces encountered in practical mechanics are two—gravity and electromagnetism, their manifestations are many, and the list above is incomplete. The electroweak and strong forces of quantum field theory are not typically encountered in practical mechanics.

Philosophical commentary

At present this is a brief observation on the question of the ‘real’.

We have an intuition of time, space, and motion. It is sufficient for some purposes.

When it was introduced, Newtonian Mechanics was the apex of classical mechanics, and for many purposes a vast improvement on intuition and the philosophy that went before. Its power was so great and application so broad that it came to be thought of as universal and real.

The theories of relativity and the quantum (field theory) vastly improve on Newtonian mechanics where the latter ‘breaks down’.

Do these modern theories capture reality?

We think—most probably not… even though many physicists and laypersons do think so.

But we have neither empirical, nor logical, nor historical reason to think so.

What we can say is, that with successive theories, there are improved descriptions of the real.

We have an intuition, which is a ‘description’ of the real.

In the material but not subjective world, Newtonian mechanics is a vast improvement over what came before.

In the Newtonian scheme, space and time are a fixed framework ‘within’ which motion occurs.

In the descriptions of general relativity, time, space, matter, and motion are interwoven. This suggests “time is not real”. What is really meant is that the time of general relativity provides a better description than the time of Newtonian mechanics.

But in quantum field considerations of gravitation, which remain speculative, suggest that the time of general relativity is not real—i.e., that there is a better description. In tentative quantum theories of gravity, time is not a continuum—rather, it is discrete.

Would quantum gravity be real? Nothing is known real until it is shown real. Should a quantum gravity emerge, it will, if accepted, provide an improved description of time and space. But again, it cannot be claimed real unless shown perfect for all (or at least sufficient) purposes.

Can we ever approach the real in our understanding? Because everything is known through the lens of our experiential or theoretical systems, we should doubt ever achieving knowledge of the real. This suggests that “the real” has no absolute meaning. However, that would appear to be false—for it does seem that at bottom the world is form and change. Can we refine and build on that?

See the way of being website (essay) for further considerations. There it is seen that at root, the world is equivalent to the void, and that form and change emerge from the void, which is found to be driven by necessity, and that relatively stable cosmoses such as ours and greater are necessary, numerically rare, but perhaps preponderant in terms of significance.

Mechanical foundations of thermodynamics

The first law

In mechanics, the terms in the equation,

generally includes only macroscopic or bulk kinetic and potential energies. Of course, all energy is molecular particle or field energy, but we can distinguish the macroscopic from the microscopic. Thus, regarding as total energy and writing it as (total energy of a system),

where designates the macroscopic or bulk part, and the internal or molecular part. The same distinctions may be made for kinetic energy, , and potential energy, .

Further, the same distinction arises for work, as work is essentially energy transfer, and may be macroscopic as well as molecular. Thus

and so, the energy equation becomes

Generally, these terms cannot be separated because the distinction between the macro and micro is imperfect.

However, while the integrity of bulk or macroscopic systems is maintained, the macro vs micro distinction is sustained.

We will then drop the subscripts and remember that the unsubscripted quantities exclude the microscopic contributions. Thus now refers only to macroscopic quantities. Similarly, we replace by .

Now introduce, the internal energy, by

and ask what the term may be. It is work done associated with microscopic motion of particles—i.e., heat. Introduce the heat transfer as

Putting these results and definitions together, obtain

This is a form of the first law of thermodynamics often used by engineers.

Now the term may be seen as having two parts, one that interacts with the macro energy , and another that interacts with the internal energy . Thus,

When is decoupled from or included in , the first law reduces to a form usually used by physicists—

Recall that is the work done on the system. In thermodynamics it is common for to be the work done by the system, and then the first law may be written in its more common form, .

Now, the above law can also be arrived at experimentally, for it is found experimentally that in a cyclic process, + is zero, and therefore must define a variable of state, which can be named .

The second law

For a simple mechanical (fluid) system, i.e., one with as pressure and volume, respectively, as the mechanical variables, the differential work done by the system in a small change is force times distance, that is,

In thermodynamics texts this equation is written , to remind readers that the process is ‘infinitesimal’. The symbol indicates that the work is not a differential of the state .

Now, if the volume of a container of the fluid were to expand suddenly, no work would be done, and the energy spent in expanding the gas to fill the container would be an acceleration and a dissipation. Thus, the equation, , presumes the process is not dissipative (see energy for discussion), otherwise and, generally, .

From the first law, writing instead of , for of , for ,

Are there variables that give analogously to for work? At zero pressure, a change in volume results in no work?

To show this remains to be done, but there are, and the, by analogy (e.g., there is no work for a change in volume at zero pressure), result is—

There are, and they are temperature , and entropy , such that

for non-dissipative processes and from which it follows that

which for simple mechanical systems, which must be true for all processes since the variables are all state variables. For a more general system, the second law may be written in the form

where and are generalized force and displacement.

Comparing and , if , then it follows that—

which is the second law of thermodynamics.